��Ŀ����
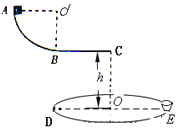
����Ŀ��ң�ص綯��߳��Ĺ��װ����ͼ��ʾ�����ABCDEF��ˮƽ���AB�κ�BD�δֲڣ�AB=BD=2.5R��С����AB��BD�����ƶ�����ʱ������������������0.02����������ಿ��Ħ�����ơ�б�沿��DE��ˮƽ����BD��Բ������EF��ƽ�����ӣ�Բ���BC�İ뾶ΪR��С��Բ��EF�İ뾶Ϊ4R��Բ���BC��ߵ�C��Բ�����EF��ߵ�F�ȸߡ�����Ҳ���������ˮƽ���AB��BD�ȸߵĿ���M��N����M�Ϳ�N���ұ�Ե��F���ˮƽ����ֱ�ΪR��2R�������ΪP������Ϊm����Ϊ�ʵ��С������AB�δ�A���ɾ�ֹ�����Զ������ʻһ��ʱ��t��tδ֪���������رյ綯����֮��С���ع����B�����Բ���������ߵ�C����B�㣬���������ξ�����D��E��F��ȫ��û��������������F��ˮƽ�ɳ���ǡ�����ڿ�N���ұ�Ե��

��1����С�����˶���F��ʱ�Թ����ѹ����
��2����С���Զ������ʻ��ʱ��t��
��3��ҪʹС������M��С����ȡ��AB�μ��٣�����ʱ��ɵ��ڣ���BD���ƶ����ٵķ�������С���ڲ���������ǰ���£���BD�������ܵ�ƽ���ƶ�������Ϊ���١�
���𰸡���1��![]() mg��������ֱ���£���2��
mg��������ֱ���£���2��![]() ����3��
����3��![]() mg
mg
��������
��1��С��ƽ���̣��У�2R=vFt����
2R=![]() gt2��
gt2��
�ɢ٢�������ã�vF=![]() ��
��
��F�㣬��С����ţ�ٵڶ����ɵã�mg��FN=m![]() ��
��
�ɢۢܵã�FN=![]() mg
mg
��ţ�ٵ������ɵ�С���Թ����ѹ����СΪ![]() mg��������ֱ���¡�
mg��������ֱ���¡�
��2��С���Ӿ�ֹ��ʼ��F��Ĺ����У��ɶ��ܶ����ã�
Pt��0.02mg![]() 5R��mg
5R��mg![]() 2R=
2R=![]() mvF2��
mvF2��
�ɢۢݵã�t=![]()
��3��ƽ�����У� R=vFt��2R=![]() gt2
gt2
ҪʹС������M��С����F�������ٶ�ΪvF=![]() ��
��
С����C����ٶ���С��ΪvC�����У�mg=m![]() ��
��
��С����BD�������ܵ��ܵ�ƽ���ƶ�������Ϊf��С����C���˶���F��Ĺ����У��ɶ��ܶ����ã�
-f![]() 2.5R=
2.5R=![]() mvF2-
mvF2-![]() mvC2��
mvC2��
�ɢޢߢ�ã�f=![]() mg
mg

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��һ�������Ӿ�ֹ��ʼ�ȼ��ٿ�����Ȼ�������˶�������ȼ����˶���ֱ��ֹͣ���±������˲�ͬʱ���������ٶȣ�
ʱ��/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
�ٶ�/ms-1 | 3 | 6 | 9 | 12 | 12 | 9 | 3 |
(1)�������������˶�ʱ�ļ��ٶȺͼ����˶�ʱ�ļ��ٶȣ�
(2)�����ӿ�����ֹͣ��������ʱ���Ƕ��٣�
(3)����ȫ�����˶��ľ����Ƕ��٣�