题目内容
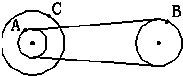如图为一皮带传动装置，大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连，它们的半径之比是1：2：3．A、B、C分别为轮子边缘上的三点，那么角速度ωA：ωB=分析：皮带传动装置，大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连，故边缘A点和B点的线速度大小相等，A点和C点有相同的角速度．根据v=ωr，求A、B两点的角速度即可求解角速度之比．根据A、B两点的角速度之比，A点和C点有相同的角速度，再利用a=ω2r，求B、C两点向心加速度之比．
解答：解：大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连，故边缘A点和B点的线速度大小相等，A点和C点有相同的角速度．根据v=ωr求A、B两点的角速度ω=
，带人数值即可求解角速度之比为2：1．根据A、B两点的角速度之比，A点和C点有相同的角速度，再利用a=ω2r，带人数值求B、C两点向心加速度之比为1：6．
故答案为：2：1；1：6．
| v |
| r |
故答案为：2：1；1：6．
点评：明确“皮带传动装置，大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连，故边缘A点和B点的线速度大小相等，A点和C点有相同的角速度”是解题的关键，灵活应用线速度、角速度、半径和向心加速度间的关系式．
练习册系列答案
相关题目
如图为一皮带传动装置，大轮与小轮固定在同一根轴上，小轮与另一中等大小的轮子间用皮带相连（皮带不打滑），它们的半径之比是1：2：3．A、B、C分别为小、中、大轮子边缘上的三点，则：
如图为一皮带传动装置，主动轮A的半径为R，从动轮B的半径为2R，P点和Q点分别位于A轮和B轮的边缘上，M点离B轮转轴为R，则（ ）
如图为一皮带传动装置的示意图．在转动过程中不打滑，RA：RB：RC=2：3：5．两皮带轮边缘上的点的线速度大小之比VA：VB：VC=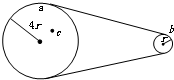
如图为一皮带传动装置．左轮半径为4r，右轮半径为r，a、b分别是左右轮边缘上的点，c点到左轮圆心的距离为2r，若传动过程中皮带不打滑，则（ ）