题目内容
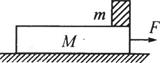
 如图所示,长为L=0.7m、质量为m=1.0kg的薄壁箱子,放在水平地面上,箱子与水平地面间的动摩擦因数μ=0.25,箱内有一质量也为m=1.0kg的小滑块,滑块与箱底间无摩擦.开始时箱子静止不动,小滑块以v0=4m/s的恒定速度从箱子的A壁处向B壁处运动,之后与B壁碰撞,滑块与箱壁每次碰撞的时间极短,可忽略不计,滑块与箱壁每次碰撞过程中,系统的机械能没有损失,g=10m/s2.求:
如图所示,长为L=0.7m、质量为m=1.0kg的薄壁箱子,放在水平地面上,箱子与水平地面间的动摩擦因数μ=0.25,箱内有一质量也为m=1.0kg的小滑块,滑块与箱底间无摩擦.开始时箱子静止不动,小滑块以v0=4m/s的恒定速度从箱子的A壁处向B壁处运动,之后与B壁碰撞,滑块与箱壁每次碰撞的时间极短,可忽略不计,滑块与箱壁每次碰撞过程中,系统的机械能没有损失,g=10m/s2.求:(1)滑块与箱壁最多可碰撞几次?
(2)从滑块开始运动到滑块与箱壁刚完成第三次碰撞的时间.
分析:(1)分析滑块和箱子的运动过程:滑块与箱子质量相等,碰撞中无机械能损失,碰撞后滑块与箱子交换速度.第一次碰撞后,箱子以速度v0开始减速运动,滑块速度变为0;当滑块速度减到v1时与滑块发生第二次碰撞,再交换速度,滑块以速度v1匀速运动,箱子静止;滑块与箱子发生第三次碰撞后,又交换速度,箱子以速度v1减速运动,木块静止;…根据动能定理列式求箱子在地面上的总位移s,即可求出滑块与箱壁的次数.
(2)分段由运动学和牛顿第二定律结合求各段时间,即可得到总时间.
(2)分段由运动学和牛顿第二定律结合求各段时间,即可得到总时间.
解答:解:(1)滑块与箱子质量相等,碰撞中无机械能损失,则碰撞后滑块与箱子交换速度.第一次碰撞后,箱子以速度v0开始减速运动,滑块速度变为0;当滑块速度减到v1时与滑块发生第二次碰撞,再交换速度,滑块以速度v1匀速运动,箱子静止;滑块与箱子发生第三次碰撞后,又交换速度,箱子以速度v1减速运动,木块静止;…
箱子的运动可以看作是初速度为v0,末速度为0的匀减速运动,在地面上的总位移为s,则由动能定理有:
-2μmgs=0-
m
代入数据,解得s=1.6m;
因为s=2L+0.2m,所以滑块与箱壁可碰撞5次.
(2)从开始到滑块与箱子碰撞前滑块做匀速运动,则从开始到第一次碰撞时间为:t1=
=0.175s;
碰后箱子减速运动的加速度为:a=
=2μg=5m/s2;
由
-
=-2aL得 v1=3m/s;
t2=
=0.2s;
t3=
=0.233s;
从开始到完成第三次碰撞的时间为:t=t1+t2+t3=0.608s.
答:
(1)滑块与箱壁最多可碰撞5次.
(2)从滑块开始运动到滑块与箱壁刚完成第三次碰撞的时间是0.608s.
箱子的运动可以看作是初速度为v0,末速度为0的匀减速运动,在地面上的总位移为s,则由动能定理有:
-2μmgs=0-
| 1 |
| 2 |
| v | 2 0 |
代入数据,解得s=1.6m;
因为s=2L+0.2m,所以滑块与箱壁可碰撞5次.
(2)从开始到滑块与箱子碰撞前滑块做匀速运动,则从开始到第一次碰撞时间为:t1=
| L |
| v0 |
碰后箱子减速运动的加速度为:a=
| 2μmg |
| m |
由
| v | 2 1 |
| v | 2 0 |
t2=
| L | ||
|
t3=
| L |
| v1 |
从开始到完成第三次碰撞的时间为:t=t1+t2+t3=0.608s.
答:
(1)滑块与箱壁最多可碰撞5次.
(2)从滑块开始运动到滑块与箱壁刚完成第三次碰撞的时间是0.608s.
点评:本题的解题关键是分析滑块与箱子的运动过程,再运用动能定理、牛顿第二定律和运动学规律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
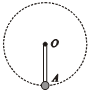 如图所示,长为L=0.5m的轻杆OA绕O点在竖直平面内做匀速圆周运动,A端连着一个质量为m=2kg的小球,取g=10m/s2.
如图所示,长为L=0.5m的轻杆OA绕O点在竖直平面内做匀速圆周运动,A端连着一个质量为m=2kg的小球,取g=10m/s2.