题目内容
4.如图甲是某物理小组验证系统的机械能是否守恒的实验装置,一端带有定滑轮的木板放置在水平桌面上,木板上有一小车,小车一端与穿过电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与钩码相连.开始时将木板固定打点计时器的一端适当垫高,在不挂钩码的条件下,轻推小车使小车能够沿木板匀速滑动.挂上钩码后,释放小车,在纸带上打出一系列小点.已知交流电源的频率为50Hz.

(1)图乙是实验中获取的一条纸带的一部分:0、1、2、3、4、5、6是计数点,每相邻两计数点间还有4个点,图中未标出.计数点间的距离x1、x2、x3、…、x6依次为:2.34c m、2.81cm、3.29cm、3.76cm、4.25cm、4.73cm.根据图中数据计算打下计数点5时的速度v5=0.449 m/s,小车运动的加速度a=0.478m/s2;(保留三位有效数字)
(2)实验中测出小车的质量为M、钩码的质量为m,计时器的打点周期为T.若不计小车沿木板运动时下降的高度,从打下计数点l到计数点5的过程中,小车和钩码组成的系统,减小的重力势能(用x1、x2、…、m、M、g和r表示)△Ep=mg(x2+x3+x4+x5),增加的动能△Ek=$\frac{1}{2}$(M+m)[($\frac{{x}_{5}+{x}_{6}}{10T}$)2-($\frac{{x}_{1}+{x}_{2}}{10T}$)2].
分析 (1)根据中间时刻的速度等于平均速度,可计算出打出某点时纸带运动的瞬时速度,利用逐差法△x=aT2可以求出物体的加速度大小;
(2)根据功能关系得重力势能减小量等于重力做功的数值.根据EK=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02求出动能的增加量.
解答 解:(1)根据中间时刻的速度等于平均速度得:
v5=$\frac{{x}_{5}+{x}_{6}}{2T}$=$\frac{0.0425+0.0473}{0.2}$=0.449m/s,
根据逐差法有:
a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$=$\frac{0.0473+0.0425+0.0376-0.0329-0.0281-0.0234}{0.09}$=0.478m/s2
(2)从打下计数点l到计数点5的过程中,小车和钩码组成的系统,
减小的重力势能△Ep=mg(x2+x3+x4+x5)
增加的动能△Ek=$\frac{1}{2}$(m+M)v52-$\frac{1}{2}$(m+M)v12=$\frac{1}{2}$(M+m)[($\frac{{x}_{5}+{x}_{6}}{10T}$)2-($\frac{{x}_{1}+{x}_{2}}{10T}$)2]
故答案为:(1)0.449;0.478;(2)mg(x2+x3+x4+x5);$\frac{1}{2}$(M+m)[($\frac{{x}_{5}+{x}_{6}}{10T}$)2-($\frac{{x}_{1}+{x}_{2}}{10T}$)2].
点评 运用运动学公式和动能、重力势能的定义式解决问题是该实验的常规问题.
要注意单位的换算和有效数字的保留.

 阅读快车系列答案
阅读快车系列答案| A. | 爱因斯坦、牛顿、亚里士多德 | B. | 牛顿、亚里士多德、爱因斯坦 | ||
| C. | 亚里士多德、爱因斯坦、牛顿 | D. | 亚里士多德、牛顿、爱因斯坦 |
| A. | 只要已知阿伏加德罗常数、某液体的摩尔质量和这种液体的质量,就可以估算出该液体的分子直径 | |
| B. | 热量可以从低温物体传递到高温物体,但一定要引起其它的变化 | |
| C. | 分子间相互作用表现为引力时,随着分子间距的增大分子间的作用力一直减小 | |
| D. | 两个分子间的距离为r0时,分子势能最小 | |
| E. | 气体的温度升高1℃,也可以说温度升高1K;温度下降5K,也就是温度下降5℃ | |
| F. | 一定质量的理想气体发生等压膨胀过程,其温度一定升高 |
| A. | 利用题中所给数据可以求出“嫦娥一号”卫星的质量 | |
| B. | “嫦娥一号”卫星绕月球极地轨道运行的加速度a=$\frac{gR}{R+h}$ | |
| C. | 月球的密度ρ=$\frac{3g}{4πGR}$ | |
| D. | “嫦娥一号”卫星在T0内绕月球极地轨道运行的圈数为$\frac{{T}_{0}}{2π}$$\sqrt{\frac{g{R}^{2}}{(R+h)^{3}}}$ |
| A. | 摩擦起电是电荷的转移 | |
| B. | 接触起电可能是产生电荷的过程 | |
| C. | 感应起电时,由于带电体和被感应导体不接触,所以一定是产生了电荷 | |
| D. | 摩擦起电和感应起电都可能是创造了电荷 |
| A. | 5:3 | B. | 7:9 | C. | 3:7 | D. | 7:8 |
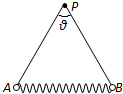 两根长度均为d=0.25m的细绳,一端系着质量均为m=0.4kg的小球A、B,另一端固定在P点,如图所示.A、B之间连接有原长l0=0.4m的轻弹簧.静止时AP、BP之间的夹角θ=74°,弹簧呈水平.g=10m/s2.求:弹簧的劲度系数k.
两根长度均为d=0.25m的细绳,一端系着质量均为m=0.4kg的小球A、B,另一端固定在P点,如图所示.A、B之间连接有原长l0=0.4m的轻弹簧.静止时AP、BP之间的夹角θ=74°,弹簧呈水平.g=10m/s2.求:弹簧的劲度系数k.