题目内容
使一小球沿半径为R的圆形轨道从最低点上升,那么需给它最小速度为多大时,才能使它达到轨道的最高点?
小球至少具有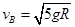 的速度,才能使它到达圆形轨道的最高点
的速度,才能使它到达圆形轨道的最高点
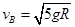 的速度,才能使它到达圆形轨道的最高点
的速度,才能使它到达圆形轨道的最高点【错解分析】错解:如图所示,
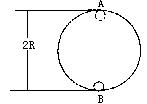
根据机械能守恒,小球在圆形轨道最高点A时的势能等于它在圆形轨道最低点B时的动能(以B点作为零势能位置),所以为
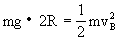
从而得
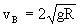
小球到达最高点A时的速度vA不能为零,否则小球早在到达A点之前就离开了圆形轨道。要使小球到达A点(自然不脱离圆形轨道),则小球在A点的速度必须满足
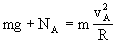 式中,NA为圆形轨道对小球的弹力。上式表示小球在A点作圆周运动所需要的向心力由轨道对它的弹力和它本身的重力共同提供。当NA=0时,
式中,NA为圆形轨道对小球的弹力。上式表示小球在A点作圆周运动所需要的向心力由轨道对它的弹力和它本身的重力共同提供。当NA=0时,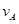 最小,
最小,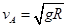 。这就是说,要使小球达到A点,则应该使小球在A点具有的速度
。这就是说,要使小球达到A点,则应该使小球在A点具有的速度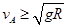 。
。【正解】以小球为研究对象。小球在轨道最高点时,受重力和轨道给的弹力。小球在圆形轨道最高点A时满足方程
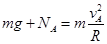 (1)
(1)根据机械能守恒,小球在圆形轨道最低点B时的速度满足方程
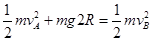 (2)
(2)解(1),(2)方程组得
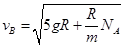
当NA=0时,vB为最小,
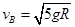 。
。所以在B点应使小球至少具有
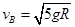 的速度,才能使它到达圆形轨道的最高点A。
的速度,才能使它到达圆形轨道的最高点A。
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目


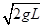
 mgL
mgL
 ,如果要使小球运动过程中不脱离圆轨道运动, v0的大小满足的条件可表示为( )
,如果要使小球运动过程中不脱离圆轨道运动, v0的大小满足的条件可表示为( )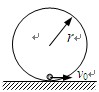
 m/s
m/s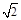 m/s
m/s