题目内容
（2012?杨浦区一模）如图所示，A、B为半径相同的两个半圆环，以大小相同、方向相反的速度运动，A环向右，B环向左，则从两半圆环开始相交到最后分离的过程中，两环交点P的速度方向和大小变化为（ ）分析：将P点的运动分解为水平方向和竖直方向，通过平行四边形定则，根据水平分速度的大小求出合速度的大小．
解答：
解：由图可知P点只在两个半圆环组成的图形的对称轴上运动．
两个半圆环刚开始相交时，P点相对地面向上运动，即速度向上．
当两个半圆环重合后，P点运动到最高点，此后P点向下运动直至两半圆环分离．
所以P的速度方向先向上再向下．至于速度把半圆直径分割成几段相等的小段（如图）．
这样可看出P点在相等的时间内运动的位移先变小再变大，即速度先变小再变大．故B正确，A、C、D错误．
故选B
解：由图可知P点只在两个半圆环组成的图形的对称轴上运动．两个半圆环刚开始相交时，P点相对地面向上运动，即速度向上．
当两个半圆环重合后，P点运动到最高点，此后P点向下运动直至两半圆环分离．
所以P的速度方向先向上再向下．至于速度把半圆直径分割成几段相等的小段（如图）．
这样可看出P点在相等的时间内运动的位移先变小再变大，即速度先变小再变大．故B正确，A、C、D错误．
故选B
点评：解决本题的关键知道P点的速度是水平分速度和竖直分速度的合速度，知道速度的合成与分解遵循平行四边形定则．注意是把直径分，因为两个半圆环是匀速运动，所以直径上相等的位移对应着相等的时间．但面积明显不等，最中间的面积最大．
练习册系列答案
阅读快车系列答案
相关题目
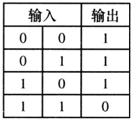（2012?杨浦区一模）如表是某逻辑电路的真值表，该电路是（ ）
（2012?杨浦区一模）如图所示，两个轻质小环A、B套在光滑固定的水平杆上，两环间距为a，用原长为L的轻质橡皮条分别连接两环（a＜l＜2a），在橡皮条中间加一竖直向上的力F，在两环上分别施加大小相等的作用力，使橡皮条拉成一个与杆围成边长为a的正三角形保持平衡，则关于施加在两环上的作用力，下列说法中正确的是（ ）
（2012?杨浦区一模）如图所示，甲、乙两物体分别从A、C两地由静止出发做加速运动，B为AC中点，两物体在AB段的加速度大小均为a1，在BC段的加速度大小均为a2，且a1＜a2．若甲由A到C所用时间为t甲，乙由C到A所用时间t乙，则t甲与t乙的大小关系为（ ）
（2012?杨浦区一模）如图所示，电路中共有100个电阻，其中：R1=R3=R5=…=R99=2Ω，R2=R4=R6=…R98=4Ω，R100=2Ω，则电路中A、B间总电阻为RAB=
（2012?杨浦区一模）如图，在倾角θ为37°的固定光滑斜面上放的一块质量不计的薄板，水平放置的棒OA，A端搁在薄板上，O端装有水平转轴，棒和板间的滑动摩擦系数为