题目内容
11. 如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.
如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(1)若小物块恰能击中档板上的P点(OP与水平方向夹角为37°,sin37°=0.6,cos37°=0.8,g=10m/s2 ),求离开O点时的速度大小;
(2)为使小物块击中档板,求拉力F作用的最短时间;
(3)改变拉力F的作用时间,使小物块击中挡板的不同位置.求击中挡板时小物块动能的最小值.
分析 (1)根据平抛运动的高度求出平抛运动的时间,再结合水平位移和时间求出物块离开O点的速度.
(2)根据动能定理求出拉力F作用的距离.
(3)根据平抛运动的知识,结合椭圆方程,根据动能定理求出击中挡板的小物块动能.
解答 解:(1)小物块从O到P,做平抛运动
水平方向:Rcos37°=v0t
竖直方向:Rsin37°=$\frac{1}{2}$gt2
解得:v0=$\frac{Rcos37°}{\sqrt{\frac{2Rsin37°}{g}}}$=$\frac{4}{3}\sqrt{3}$m/s
(2)为使小物块击中档板,小物块必须恰好能运动到O点,
由动能定理得:Fx-μmgS=△Ek=0
解得:x=2.5m
由牛顿第二定律得:F-μmg=ma
解得:a=5m/s2
由运动学公式得:x=$\frac{1}{2}$at2
解得:t=1s
(3)设小物块击中挡板的任意点坐标为(x,y),则x=v0t
y=$\frac{1}{2}$gt2
由机械能守恒得:Ek=$\frac{1}{2}$m${v}_{0}^{2}$+mgy
又x2+y2=R2
化简得:Ek=$\frac{mg{R}^{2}}{4y}$+$\frac{3mgy}{4}$
由数学方法求得:Ekmin=$\frac{5}{2}\sqrt{3}$J
答:(1)其离开O点时的速度大小为:$\frac{4}{3}\sqrt{3}$m/s;
(2)为使小物块击中档板,拉力F作用的最短时间1s;
(3)改变拉力F的作用时间,使小物块击中挡板的不同位置.击中挡板时小物块动能的最小值为$\frac{5}{2}\sqrt{3}$J.
点评 本题综合了动能定理和平抛运动知识,综合性较强,难度中等,知道平抛运动在水平方向上和竖直方向上的运动规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图所示,在甲、乙两个相同的水平圆盘上,分别沿半径方向放置用长度相同的细线相连质量均为m的小物体A(位于转轴处)、B和C、D,它们与圆盘之间的动摩擦因数相等.当甲、乙的角速度缓缓增大到B、D恰好将要相对圆盘滑动时,则下列说法中错误的是( )
如图所示,在甲、乙两个相同的水平圆盘上,分别沿半径方向放置用长度相同的细线相连质量均为m的小物体A(位于转轴处)、B和C、D,它们与圆盘之间的动摩擦因数相等.当甲、乙的角速度缓缓增大到B、D恰好将要相对圆盘滑动时,则下列说法中错误的是( )
 如图所示,在甲、乙两个相同的水平圆盘上,分别沿半径方向放置用长度相同的细线相连质量均为m的小物体A(位于转轴处)、B和C、D,它们与圆盘之间的动摩擦因数相等.当甲、乙的角速度缓缓增大到B、D恰好将要相对圆盘滑动时,则下列说法中错误的是( )
如图所示,在甲、乙两个相同的水平圆盘上,分别沿半径方向放置用长度相同的细线相连质量均为m的小物体A(位于转轴处)、B和C、D,它们与圆盘之间的动摩擦因数相等.当甲、乙的角速度缓缓增大到B、D恰好将要相对圆盘滑动时,则下列说法中错误的是( )| A. | 若突然剪断细线,A仍静止,B向外滑动 | |
| B. | 若突然剪断细线,C仍静止,D向外滑动 | |
| C. | 若突然剪断细线,C、D均向外滑动 | |
| D. | 当角速度继续增加时,C、D均将向外滑动 |
16. 如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下加速上升的一段时间内,( )
如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下加速上升的一段时间内,( )
 如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下加速上升的一段时间内,( )
如图所示,竖直放置的两根平行金属导轨之间接有定值电阻R,质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦,棒与导轨的电阻均不计,整个装置放在匀强磁场中,磁场方向与导轨平面垂直,棒在竖直向上的恒力F作用下加速上升的一段时间内,( )| A. | 作用于金属棒上的各个力的合力所作的功等于零 | |
| B. | 作用于金属棒上的各个力的合力所作的功等于棒的机械能增量与电阻上产生焦耳热之和 | |
| C. | 恒力F做的功与安培力做的功的代数和等于棒的机械能增加量 | |
| D. | 恒力F与重力的合力所作的功大于电阻R上发出的焦耳热 |
3.物体作匀加速直线运动,已知加速度为2m/s2,下列说法正确的是( )
| A. | 那么任意1秒时间内,物体的末速度一定等于初速度的2倍 | |
| B. | 那么任意1秒时间内,物体的末速度一定比初速度大2m/s | |
| C. | 第5s的初速度一定比第4 s的末速度大2m/s | |
| D. | 第5s的末速度一定比第4s的初速度大4m/s |
20.某车队从同一地点先后从静止开出n辆汽车,在平直的公路上沿一直线行驶,各车均先做加速度为a的匀加速直线运动,达到速度v后做匀速直线运动,汽车都匀速行驶后,相邻两车距离均为s,则相邻两车启动的时间间隔为( )
| A. | $\frac{2v}{a}$ | B. | $\frac{v}{2a}$ | C. | $\frac{s}{2v}$ | D. | $\frac{s}{v}$ |
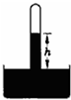 一端封闭的玻璃管开口向下插入水银槽内,如图所示,管内水银柱比槽内水银面高h=5cm,空气柱长L=45cm,要使管内外水银面相平.求:
一端封闭的玻璃管开口向下插入水银槽内,如图所示,管内水银柱比槽内水银面高h=5cm,空气柱长L=45cm,要使管内外水银面相平.求: 一物体的质量为10kg,在水平推力F=200N的作用下,从粗糙斜面的底端由静止开始沿斜面向上运动,斜面固定不动,与水平地面的夹角θ=37°,力F作用2秒钟后撤去,物体在斜面上继续上滑了1.25秒钟后停下来,求:
一物体的质量为10kg,在水平推力F=200N的作用下,从粗糙斜面的底端由静止开始沿斜面向上运动,斜面固定不动,与水平地面的夹角θ=37°,力F作用2秒钟后撤去,物体在斜面上继续上滑了1.25秒钟后停下来,求: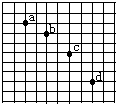 如图所示,在“研究平抛物体运动”的实验中:
如图所示,在“研究平抛物体运动”的实验中: