题目内容
16．
如图所示，竖直放置的两根平行金属导轨之间接有定值电阻R，质量不能忽略的金属棒与两导轨始终保持垂直并良好接触且无摩擦，棒与导轨的电阻均不计，整个装置放在匀强磁场中，磁场方向与导轨平面垂直，棒在竖直向上的恒力F作用下加速上升的一段时间内，（ ）| A． | 作用于金属棒上的各个力的合力所作的功等于零 | |
| B． | 作用于金属棒上的各个力的合力所作的功等于棒的机械能增量与电阻上产生焦耳热之和 | |
| C． | 恒力F做的功与安培力做的功的代数和等于棒的机械能增加量 | |
| D． | 恒力F与重力的合力所作的功大于电阻R上发出的焦耳热 |
分析 棒在竖直向上的恒力F作用下加速上升的一段时间内，F做正功，安培力做负功，重力做负功，动能增大．根据动能定理分析力F做的功与安培力做的功的代数和．
解答 解：A、棒在竖直向上的恒力F作用下加速运动，动能增加，由动能定理得知合力所做的功大于零，故A错误．
B、棒受重力G、拉力F和安培力FA的作用，由动能定理知，等于合力所做的功等于棒的动能增加量，故B错误．
C、由动能定理得：WF-mgh-W安=△EK，则WF-W安=△EK+mgh，即力F做的功与安培力做功的代数和等于机械能的增加量，故C正确．
D、由动能定理：WF-mgh-W安=△EK，则WF-mgh=W安+△EK=Q+△EK，即恒力F与重力的合力所作的功大于电阻R上发出的焦耳热，故D正确；
故选：CD
点评 本题运用功能关系分析实际问题．对于动能定理理解要到位：合力对物体做功等于物体动能的增量，哪些力对物体做功，分析时不能遗漏．
练习册系列答案
相关题目
3．
如图所示光滑管形圆轨道半径为R（管径远小于R），小球a、b大小相同，质量均为m，其直径略小于管径，能在管中无摩擦运动，两球先后以相同的速度v通过轨道最低点，且当小球a在最低点时，小球b在最高点，以下说法不正确的是（ ）
如图所示光滑管形圆轨道半径为R（管径远小于R），小球a、b大小相同，质量均为m，其直径略小于管径，能在管中无摩擦运动，两球先后以相同的速度v通过轨道最低点，且当小球a在最低点时，小球b在最高点，以下说法不正确的是（ ）| A． | 当小球b在最高点对轨道无压力时，小球a比小球b所需向心力大5mg | |
| B． | 当v=$\sqrt{5gR}$时，小球b在轨道最高点对轨道无压力 | |
| C． | 速度v只至少为2$\sqrt{gR}$，才能使两球在管内做圆周运动 | |
| D． | 只要v≥$\sqrt{5gR}$，小球a对轨道最低点的压力比小球b对轨道最高点的压力大6mg |
4．
如图所示，甲带负电，乙是足够长的不带电的绝缘木板，甲、乙叠放在一起置于粗糙的地板上，空间有垂直纸面向里的匀强磁场，用水平恒力F拉乙物块，使甲、乙从静止开始向左运动，在甲运动达到稳态的过程中（ ）
如图所示，甲带负电，乙是足够长的不带电的绝缘木板，甲、乙叠放在一起置于粗糙的地板上，空间有垂直纸面向里的匀强磁场，用水平恒力F拉乙物块，使甲、乙从静止开始向左运动，在甲运动达到稳态的过程中（ ）| A． | 甲、乙间的摩擦力不断增大 | B． | 甲、乙间的摩擦力不断减小 | ||
| C． | 甲、乙间摩擦力先增后减直至为零 | D． | 乙物块与地面间的摩擦力不断减小 |
如图所示，在粗糙水平台阶上静止放置一质量m=0.5kg的小物块，它与水平台阶表面的动摩擦因数μ=0.5，且与台阶边缘O点的距离s=5m．在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板，圆弧半径R=1m，今以O点为原点建立平面直角坐标系．现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板．
如图所示，MPQO为有界的竖直向下的匀强电场，电场强度为E，ACB为光滑固定的半圆形轨道，轨道半径为R，A、B为圆水平直径的两个端点，AC为$\frac{1}{4}$圆弧．一个质量为m，电荷量为+q的带电小球，从A点正上方高为H处由静止释放，并从A点沿切线进入半圆轨道．不计空气阻力及一切能量损失．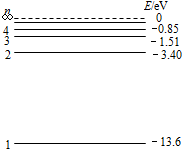
1930年泡利提出，在β衰变中除了电子外还会放出不带电且几乎没有静质量的反中微子$\overline{{v}_{e}}$．氚是最简单的放射性原子核，衰变方程为${\;}_{1}^{3}$H→${\;}_{2}^{3}$He+${\;}_{-1}^{0}$e+$\overline{{v}_{e}}$，半衰期为12.5年．下列说法中正确的是B
某学习小组设计了一种粗测小物体质量的方法．使用的器材有细绳、硬纸板、支架、刻度尺、铅笔、白纸、自制小滑轮、已知质量的小物块和若干待测小物体等．
如图所示，质量为1kg的物体以10m/s在的初速度从A点向斜面底端B点水平运动，然后再滑上倾角为30°的斜面，若已知物体与水平面和斜面的动摩擦因数均为$\frac{\sqrt{3}}{5}$，A与B的距离为L=2$\sqrt{3}$m，斜面足够长，且物体在B点时无动能损失．（g取10m/s2） 试求：