��Ŀ����
1��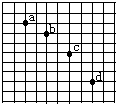 ��ͼ��ʾ���ڡ��о�ƽ�������˶�����ʵ���У�
��ͼ��ʾ���ڡ��о�ƽ�������˶�����ʵ���У���1����װʵ��װ�ù����У�б��ĩ�˵����߱�����ˮƽ�ģ���������Ŀ���ǣ�C
A����֤С���˶��Ĺ����һ��������
B����֤С���ڿ����˶���ʱ��ÿ�ζ����
C����֤С��ɳ�ʱ�����ٶ�ˮƽ
D����֤С��ɳ�ʱ���ٶȼȲ�̫��Ҳ��̫С
��2����ͼ��ʾ����ʵ���У���һ��ӡ��С�����ֽ��¼�켣��С����ı߳�l=4.0��10-3m����С����ƽ���˶���ͼ�еļ���λ����ͼ�е�a��b��c��d��ʾ����С��ƽ�ij��ٶȵļ���ʽΪvo=$\sqrt{2gl}$����l��g��ʾ������ֵ��0.4m/s��ȡg=10m/s2����
���� ��1����ʵ������С���ڹ̶�б�۹��º���ƽ���˶�����¼��ƽ���˶��켣��Ȼ�����˶��켣�ϱ������㣬�Դ˽��д�����������ͬһ���켣�����Ҫ���׳���С����ٶ�����ͬ�ģ�������ʵ��ʱ����ȷ���׳��ٶȷ�����ˮƽ�ģ�ͬʱ�̶���б��Ҫ����ֱ�森
��2��ƽ���˶�ˮƽ��������ֱ���˶�����ֱ�������������˶���������ͻ�ƿ�����������ֱ�������������ʱ���ڵ�λ�Ʋ���ڳ�������������ڣ�Ȼ���һ�������ȱ���ֱ���˶��Ĺ��ɡ�������⣮
��� �⣺��1���о�ƽ���˶���ʵ��ܹؼ��ĵط���Ҫ��֤С���ܹ�ˮƽ�ɳ���ֻ��ˮƽ�ɳ�ʱС�����ƽ���˶�����ABD����C��ȷ��
��ѡ��C��
��2�����ݡ�y=gT2�ã�T=$\sqrt{\frac{��y}{g}}=\sqrt{\frac{l}{g}}$��
ˮƽ���������˶�������У�x=2l=v0T������ٶ�${v}_{0}=\frac{x}{T}=2\sqrt{gl}$��
�������ݵã�${v}_{0}=2\sqrt{10��4��1{0}^{-3}}=0.4m/s$
�ʴ�Ϊ����1��C����2��$\sqrt{2gl}$��0.4m/s
���� ��ʵ�������ʵ����С����ƽ���˶��ǹؼ������ʵ���йؼ���б��ĩ�˲ۿڵ����߱���ˮƽ���̶����б��Ҫ��ֱ������ƽ���˶����⣬һ����ȷ��ˮƽ����ֱ�����˶��ص㣬����������ֱ��������Ӧ���ȱ���ֱ���˶��Ĺ��ɺ����۽⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | P1=mg2t2��P2=$\frac{1}{2}$mg2t2 | B�� | P1=mg2t2��P2=mg2t2 | ||
| C�� | P1=$\frac{1}{2}$mg2t��P2=mg2t | D�� | P1=mg2t2��P2=2mg2t2 |
| A�� | $\frac{1}{5}$mv | B�� | mv | C�� | $\frac{4}{5}$mv | D�� | $\frac{9}{5}$mv |
| A�� | ����д����ٶ���ͬ | |
| B�� | ���ܷ������䡢���䡢��������� | |
| C�� | ��������������Ľ��� | |
| D�� | ��������·�����ɵ��ӵ��˶������� |
 ��ͼ��ʾ���ڴֲ�ˮƽ̨���Ͼ�ֹ����һ����m=0.5kg��С��飬����ˮƽ̨�ױ���Ķ�Ħ��������=0.5������̨�ױ�ԵO��ľ���s=5m����̨���Ҳ�̶���һ��$\frac{1}{4}$Բ�����壬Բ���뾶R=1m������O��Ϊԭ�㽨��ƽ��ֱ������ϵ������F=5N��ˮƽ��������С��飬һ��ʱ���ȥ������С�������ˮƽ�׳������е��壮
��ͼ��ʾ���ڴֲ�ˮƽ̨���Ͼ�ֹ����һ����m=0.5kg��С��飬����ˮƽ̨�ױ���Ķ�Ħ��������=0.5������̨�ױ�ԵO��ľ���s=5m����̨���Ҳ�̶���һ��$\frac{1}{4}$Բ�����壬Բ���뾶R=1m������O��Ϊԭ�㽨��ƽ��ֱ������ϵ������F=5N��ˮƽ��������С��飬һ��ʱ���ȥ������С�������ˮƽ�׳������е��壮 ��ͼ��ʾ������Ϊ1kg��������10m/s�ڵij��ٶȴ�A����б���B��ˮƽ�˶���Ȼ���ٻ������Ϊ30���б�棬����֪������ˮƽ���б��Ķ�Ħ��������Ϊ$\frac{\sqrt{3}}{5}$��A��B�ľ���ΪL=2$\sqrt{3}$m��б���㹻������������B��ʱ������ʧ����gȡ10m/s2�� ����
��ͼ��ʾ������Ϊ1kg��������10m/s�ڵij��ٶȴ�A����б���B��ˮƽ�˶���Ȼ���ٻ������Ϊ30���б�棬����֪������ˮƽ���б��Ķ�Ħ��������Ϊ$\frac{\sqrt{3}}{5}$��A��B�ľ���ΪL=2$\sqrt{3}$m��б���㹻������������B��ʱ������ʧ����gȡ10m/s2�� ����