Question

【题目】如图，两个质点P、Q在光滑的水平面上分别以一定的速度同时向右运动，此时分别作用水平向左的力F1、F2，其中F1的大小不变，F2大小由零逐渐增大，它们恰好同时向右运动到最远，且位移大小相等，在此过程中，两质点的瞬时速度vP与vQ的关系应该是(　　)

A. vP > vQ

B. 先vP > vQ，后vP < vQ ，最后vP = vQ = 0

C. vP < vQ

D. 先vP < vQ，后vP > vQ，最后vP = vQ = 0

Answer 1

【答案】B

【解析】

两个质点运动的的vt图象如图所示。

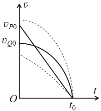
在vt图象上，任一点的切线的斜率数值上等于在该时刻的加速度，由于Q的加速度由零不断增大，曲线切线斜率的绝对值也应从零开始不断增大，即曲线的切线应从水平状态开始不断变陡，那么只有向右边凸出的下降的曲线才能满足这样的条件，又因Q与P的运动时间相等，所以曲线的终点也应在t0，Q与P的运动位移大小相等，所以曲线包围的面积应等于ΔP0Ot0的面积，根据这些要求，曲线的起点，即质点Q的初速度vQ0必定小于P点的初速度vP0，且两条vt图象必定会相交，如图中的实线所示，图中的两条虚线表示的质点Q的vt图象都不满足题设条件(P与Q的位移大小相等)，所以B正确。故选B。