题目内容
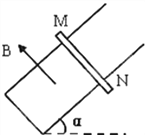
【题目】如图所示，导轨间距L=0.5m，α=37°，B=0.8T，棒的质量为m=0.2kg，金属棒的电阻为R=2Ω，其余电阻不计，金属棒与导轨的动摩擦因数μ=0.5，导体棒由静止开始运动，到刚好匀速时，通过导体横截面的电量Q=2C．求：
(1)棒在运动过程中，任意△t=2s内导体棒在框架上可能扫过的最大面积；
(2)从开始下滑到刚好匀速，导体棒中产生的焦耳热（g=10m/s2）.
【答案】(1)
(2)Q=1.5J
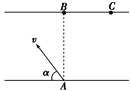
【解析】（1）金属棒运动时产生的电动势方向从N到M，匀速时，对金属棒受力分析如图，应满足：mgsinα=μmgcosα+F安①
根据法拉第电磁感应定律应有：E=BLv②
根据闭合电路欧姆定律应有：I=E/R③
又F安=BIL④
联立①②③④可得：v=5m/s⑤
由于金属棒匀速时速度最大，所以在△t时间内扫过的最大面积为：Smax=Lv△t=0.5×5×2m2=5m2
（2）根据电量
，
以及
仁爱英语同步练习册系列答案
学习实践园地系列答案
【题目】利用图甲装置做“验证机械能守恒定律”实验，从图示位置开始释放重锤。
（1）请指出图甲中的错误及不妥之处（只需写出两处）。
① ② ；
（2）改进实验中错误及不妥之处后，某同学经正确操作得到打点纸带，在纸带后段每两个计时间隔取一个计数点，依次为1、2、3、4、5、6、7，测量各计数点到第一个打点的距离h，并正确求出打相应点时的速度v．各计数点对应的数据见下表：
计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
h（m） | 0．124 | 0．194 | 0．279 | 0．380 | 0．497 | 0．630 | 0．777 |
v（m/s） | 1．94 | 2．33 | 2．73 | 3．13 | 3．50 | ||
v2（m2/s2） | 3．76 | 5．43 | 7．45 | 9．80 | 12．30 |
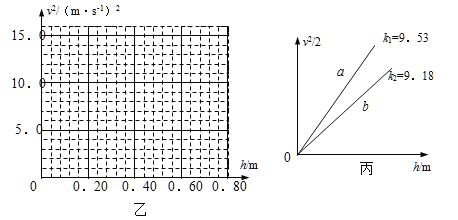
请在图乙坐标中，描点作出v2～h图线；由图线可知，重锤下落的加速度g′= m/s2（保留三位有效数字）；若当地的重力加速度g= 9．80m/s2，根据作出的图线，能粗略验证自由下落的重锺机械能守恒的依据 ．
（3）某同学选用两个形状相同质量不同的重物a和b进行实验测得几组数据，画出
的图象如图丙所示，求出图线的斜率k，由图象可知a的质量m1 b的质量m2（选填“大于”或“小于”）。造成以上原因是实验过程中存在各种阻力，已知实验所用重物的质量m2=0．052kg，当地重力加速度g=9．78m/s2，则重物所受的平均阻力f= N。（结果保留两位有效数字）
