题目内容
14.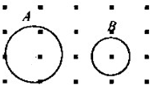 如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为${n}_{2}^{\;}:{n}_{1}^{\;}$.
如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为${n}_{2}^{\;}:{n}_{1}^{\;}$.
分析 由法拉第电磁感应定律$E=n\frac{△Φ}{△t}=n\frac{△B}{△t}π{R}_{\;}^{2}$,求解感应电动势之比.根据电阻定律:电阻$r=ρ\frac{L}{S}$,感应电流$I=\frac{E}{r}$,联立求解感应电流之比.
解答 解:由法拉第电磁感应定律得:$E=n\frac{△Φ}{△t}=n\frac{△B}{△t}π{R}_{\;}^{2}$,可知,感应电动势与半径的平方成正比,而根据电阻定律,线圈的电阻为:$r=ρ\frac{L}{S}=ρ\frac{n•2πR}{S}$
线圈中感应电流$I=\frac{E}{r}$,由上综合得到,感应电流与线圈半径成正比,即${I}_{A}^{\;}:{I}_{B}^{\;}={R}_{A}^{\;}:{R}_{B}^{\;}$;
因相同导线绕成匝数分别为n1和n2的圆形线圈,因此半径与匝数成反比,故IA:IB=n2:n1;
故答案为:n2:n1
点评 本题是法拉第电磁感应定律和电阻定律的综合应用求解感应电流之比,采用比例法研究.

练习册系列答案
相关题目
2. 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面间的电势差相等,实线为一带正电的质点仅在电场力作用下的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,c的电势较高 | B. | 带电质点通过Q点时的电势能较大 | ||
| C. | 带电质点通过P点时的动能较大 | D. | 带电质点通过Q点时的加速度较大 |
9.如图所示,电源电动势为E,内阻为r,当电建K闭合时,各电表示数变化为( )


| A. | A1变小,A2变大,V1变小,V2变大 | B. | A1变大,A2变小,V1变大,V2变小 | ||
| C. | A1变小,A2变大,V1变小,V2变大 | D. | A1变大,A2变小,V1变大,V2变大 |
3. 如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )
如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )
 如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )
如图所示,质量为m的物体,在水平外力F作用下,以速度v沿水平面匀速运动,当物体运动到A点时撤去外力F,物体由A点继续向前滑行的过程中经过B点,则物体由A点到B点的过程中,下列说法正确的是( )| A. | v越大,摩擦力对物体的冲量越大;摩擦力做功越多 | |
| B. | v越大,摩擦力对物体的冲量越大;摩擦力做功与v的大小无关 | |
| C. | v越大,摩擦力对物体的冲量越小;摩擦力做功越少 | |
| D. | v越大,摩擦力对物体的冲量越小;摩擦力做功与v的大小无关 |
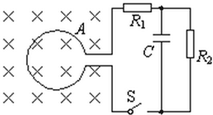 横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
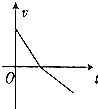
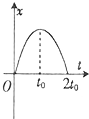
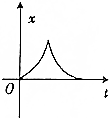
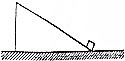 如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )
如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )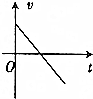
 在“描绘小灯泡的伏安特性曲线”的实验中,可供选择的器材及代号如下:
在“描绘小灯泡的伏安特性曲线”的实验中,可供选择的器材及代号如下: