题目内容
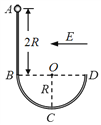
【题目】如图，横截面为圆形的绝缘杆ABCD固定在竖直平面内，其中AB是高度为2R的粗糙直杆，BCD是半径为R的光滑半圆形杆，BD是水平的直径、C为最低点。一个质量为m、中间开有圆孔的带电小球套在杆上，球孔直径略大于杆的直径，空间中存在方向水平向左的匀强电场，电场强度大小为E。小球从直杆上端A由静止释放，经过B点和C点时的动能都等于
(g为重力加速度)、已知小球运动过程所带电荷量保持不变，绝缘杆不带电。
(1)求小球的电荷量q并说明电荷的正负；
(2)求小球与直杆之间的动摩擦因数
；
(3)若在A点给小球一定的初速度，使小球能运动至半圆形杆的右端点D，则初速度v0至少多大？
【答案】（1）
小球带正电，（2）
（3）
【解析】（1）小球从B点运动到C点过程，动能改变量为0，由动能定理得
mgR-qER=0 ①
解得小球的电荷量Q=mg/E （小球带正电） ②
（2）小球从A点运动到B点过程，由动能定理得
③
解得小球与直杆之间的动摩擦因数μ=0.25 ④
（3）小球从A点开始运动恰好能到达D点，有
⑤
解得初速度至少为 ⑥
练习册系列答案
相关题目
