题目内容
1. 如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.
如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.
分析 根据万有引力定律求出M对m的万有引力,当从M中挖去一半径为r=$\frac{1}{2}$R的球体时,剩下部分对m的万有引力等于原来的万有引力减去被挖去的球体对m的万有引力.
解答 解:质点与大球球心相距2R,其万有引力为F1,则有:F1=$G\frac{Mm}{(2R)^{2}}=\frac{1}{4}G\frac{Mm}{{R}^{2}}$
大球质量为:M=ρ×$\frac{4}{3}$πR 3,
挖去的小球质量为:M′=ρ×$\frac{4}{3}$π($\frac{R}{2}$)3,
即M′=$\frac{1}{8}$ρ×$\frac{4}{3}$πR3=$\frac{M}{8}$
小球球心与质点间相距$\frac{3}{2}R$,小球与质点间的万有引力为:
F1′=$G\frac{M′m}{(\frac{3}{2}R)^{2}}=\frac{1}{18}G\frac{Mm}{{R}^{2}}$
则剩余部分对质点m的万有引力为:
F2=F1-F1′=$\frac{1}{4}G\frac{Mm}{{R}^{2}}$-$\frac{1}{18}G\frac{Mm}{{R}^{2}}$=$\frac{7}{36}G\frac{Mm}{{R}^{2}}$
故有:$\frac{{F}_{1}}{{F}_{2}}=\frac{9}{7}$.
答:$\frac{{F}_{1}}{{F}_{2}}=\frac{9}{7}$.
点评 本题主要考查了万有引力定律得直接应用,注意球体对质点的距离为球心到质点的距离.

练习册系列答案
相关题目
11.在某段电路中,其两端电压为U,通过电路电流为I,通电时间为t,关于电功和电热说法正确的是( )
| A. | 在任何电路中,电功UIt等于电热I2Rt | |
| B. | 在任何电路中,电功等于UIt,电热等于I2Rt | |
| C. | 在纯电阻电路中,电功大于电热 | |
| D. | 电流通过电动机时,电动机工作的电功等于电热 |
12.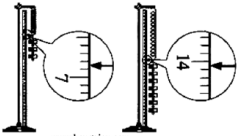 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
②实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm、d2=L5-L1=6.90cm、d3=L6-L3=7.00,请你给出第四个差值:dA=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{({d}_{1}+{d}_{2}+{d}_{3}+{d}_{4})}{4×4}$,代入数据解得:△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm、d2=L5-L1=6.90cm、d3=L6-L3=7.00,请你给出第四个差值:dA=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{({d}_{1}+{d}_{2}+{d}_{3}+{d}_{4})}{4×4}$,代入数据解得:△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
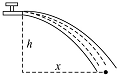 2010年3月22日是第18届“世界水日”,联合国确定的宣传主题是“清洁用水,健康用水”.我国是水资源严重缺乏的国家,节约用水是一项基本国策.土地浇灌时,由大水漫灌改为喷灌,能够节约很多淡水.如图所示的是推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,它沿水平方向把水喷出的距离为x,设“水龙头”的直径为d,则此喷水“龙头”的流量为$\frac{πx{d}^{2}}{4}\sqrt{\frac{g}{2h}}$.
2010年3月22日是第18届“世界水日”,联合国确定的宣传主题是“清洁用水,健康用水”.我国是水资源严重缺乏的国家,节约用水是一项基本国策.土地浇灌时,由大水漫灌改为喷灌,能够节约很多淡水.如图所示的是推行节水工程的转动喷水“龙头”,“龙头”距地面高为h,它沿水平方向把水喷出的距离为x,设“水龙头”的直径为d,则此喷水“龙头”的流量为$\frac{πx{d}^{2}}{4}\sqrt{\frac{g}{2h}}$.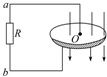 如图所示,金属圆盘可绕O轴转动,电阻R用电刷接于圆盘中心和边缘之间.当圆盘做顺时针方向的转动时(从上向下看),通过R的电流方向是b→a.
如图所示,金属圆盘可绕O轴转动,电阻R用电刷接于圆盘中心和边缘之间.当圆盘做顺时针方向的转动时(从上向下看),通过R的电流方向是b→a.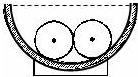 如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)
如图所示,两个质量均为0.4kg的光滑球,其半径均为r=3cm,将其放置在光滑半球形碗底,半球形碗口各处处于同一水平面上.两球最终在半径R=8cm的光滑半球形碗底稳定后处于静止状态,求两球之间相互作用力的大小(取g=10m/s2,sin 37°=0.6,cos 37°=0.8)