题目内容
如图所示,线的上端固定,下端系一小球,将小球与线拉在同一水平位置后从静止开始释放,求小球的摆线运动到与水平方向成多大角度时,小球所受的重力的功率最大.(用反三角函数表示)
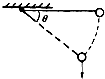

设小球下摆动θ角,只有重力做功机械能守恒 mglsinθ=
mv2 ①
小球做圆周运动满足:T-mgsinθ=m
…②
要使竖直方向速度最大则有:Tsinθ=mg…③
由①、②、③得:sin2θ=
θ=arcsin
小球竖直方向最大速度为vy=vcosθ=
cosθ=
.
答:小球的摆线运动到与水平方向成arcsin
,重力功率最大
| 1 |
| 2 |
小球做圆周运动满足:T-mgsinθ=m
| v2 |
| l |
要使竖直方向速度最大则有:Tsinθ=mg…③
由①、②、③得:sin2θ=
| 1 |
| 3 |
θ=arcsin
| ||
| 3 |
小球竖直方向最大速度为vy=vcosθ=
| 2glsinθ |
| 2 |
| 3 |
gl
|
答:小球的摆线运动到与水平方向成arcsin
| ||
| 3 |

练习册系列答案
相关题目

