��Ŀ����
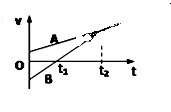
����Ŀ��A��B������ͬһֱ�������������˶���B���� A��ǰ��A�����ٶȴ�СΪ v1=8m/s��B�����ٶȴ�СΪ V2=20m/s����ͼ��ʾ���� A��B�������x0=28mʱ��B����ǰ��ͻ���������ɲ������֪ɲ�����̵��˶�����Ϊ�ȼ���ֱ���˶��������ٶȴ�СΪa=2m/s2 �� �Ӵ�ʱ��ʼ��ʱ����
��1��A����B��֮ǰ���������������룮
��2��A����B�����õ�ʱ�䣮
���𰸡�
��1���⣺����λ�ƹ�ϵ����A����B������ʱ�䣻
����λ�ƹ�ʽ�ã�xA=v1 t1
![]()
��xm=xB+xo��xA
�������ݽ�ã���xm=64 m
��A����B��֮ǰ����������������Ϊ64m��
��2���⣺B��ɲ��ֹͣ�˶�����ʱ�䣺to= ![]() =10 s
=10 s
������λ�ƣ�xB= ![]() =100m
=100m
��ʱ��xA=v1 t0=80m
��xA��x0+xB���ɼ���ʱA����δ��B����������B��ֹͣ�����
֮��A���˶�ʱ��Ϊ��t2= ![]() =6 s
=6 s
������ʱ��Ϊ��t=to+t2=16 s
��A����B�����õ�ʱ��Ϊ16s��
���������⣺��1����A��B�����ٶ����ʱ�������Զ
�����ٶȹ�ϵ�ã�v1=v2��a t1
��ã�t1=6 s
��1�������ٶ����ʱ����ǰ��������ٽ��������ݴ˷�����������뼴�ɣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ