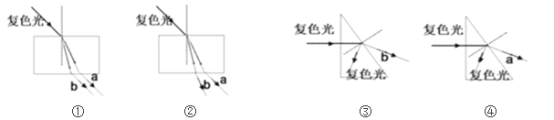
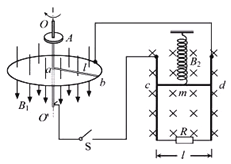
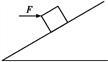
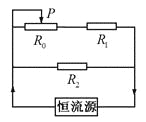
��Ŀ����
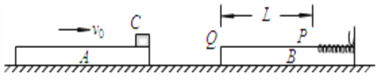
����Ŀ����ͼ��ʾ,����״��ȫ��ͬ��ƽ��A��B���ڹ⻬ˮƽ����,�����ֱ�Ϊm��2m.ƽ��B���Ҷ˹̶�һ���ʵ���,P��Ϊ���ɵ�ԭ��λ��,P�㵽ƽ��B��˵�Q�ľ���ΪL.���C����ƽ��A�����Ҷ�,����Ϊm�ҿ���Ϊ�ʵ�.ƽ��A�����C����ͬ�ٶ������˶�,�뾲ֹƽ��B������ײ,��ײʱ�伫��,��ײ��ƽ��A��Bճ����һ��,���C����ƽ��B,�˶���P�㿪ʼѹ������,���ز������ƽ��B��ֹ�������Q��.����ʼ���ڵ�������,ƽ��B��P���Ҳಿ��Ϊ�⻬��,P����ಿ��Ϊ�ֲ���,���C��ƽ��B�ֲ��沿��֮��Ķ�Ħ������������ͬ,�������ٶ�Ϊg.��:
(1)���C��ƽ��B�ֲ��沿��֮��Ķ�Ħ������![]() ;
;
(2)������������,ϵͳ�����������![]() .
.
���𰸡���1��![]() ��2��
��2��![]()
����������1��ȡA��B��CΪϵͳ����A��B��ײ�Ĺ��̣����ݶ����غ㶨�ɣ��У� ![]() =��m+2m��
=��m+2m��![]()
��ã� ![]() =
=![]()
��C������Q��ʱA��B��C��ͬ�ٶ�Ϊ![]() �����ݶ����غ㶨�ɣ��У�2m
�����ݶ����غ㶨�ɣ��У�2m![]() =4 m
=4 m![]() ��
��
��ã� ![]() =
=![]()
��A��B��C��ɵ�ϵͳ����A��B��ײ����˲ʱ��C���յ���Q��Ĺ��̣����������غ㶨�ɣ��У� ![]() ��
��
��ã� ![]() =
=![]()
��2���赯��ѹ�������ʱA��B��C��ͬ�ٶ�Ϊ![]() ������A��B��C��ɵ�ϵͳ������ѹ�������ʱϵͳ��������
������A��B��C��ɵ�ϵͳ������ѹ�������ʱϵͳ��������![]() ���ȡ��A��B��ײ��˲�䵽����ѹ������̵Ĺ��̣��ɶ����غ㶨���У�2m
���ȡ��A��B��ײ��˲�䵽����ѹ������̵Ĺ��̣��ɶ����غ㶨���У�2m![]() =4 m
=4 m![]() ��
��
���![]() =
=![]()
�ɾ������غ㶨���У� ![]()
��ã� ![]() =
=![]() m
m![]()