题目内容
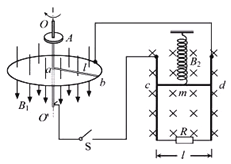
【题目】为了探究电动机转速与弹簧伸长量之间的关系,小明设计了如图所示的装置.半径为l的圆形金属导轨固定在水平面上,一根长也为l,电阻为R的金属棒ab一端与导轨接触良好,另一端固定在圆心处的导电转轴00"上,由电动机A带动旋转。在金属导轨区域内存在垂直于导轨平面,大小为B1、方向竖直向下的匀强磁场。另有一质量为m、电阻为R的金属棒cd用轻质弹簧悬挂在竖直平面内,并与固定在竖直平面内的“U”型导轨保持良好接触,导轨间距为l,底部接阻值也为R的电阻,处于大小为B2、方向垂直导轨平面向里的匀强磁场中。从圆形金属导轨引出导线和通过电刷从转轴引出导线经开关S与“U”型导轨连接。当开关S断开,棒cd静止时,弹簧伸长量为x0;当开关S闭合,电动机以某一转速匀速转动,棒cd再次静止时,弹簧伸长量变为x(不超过弹性限度)。不计其余电阻和摩擦等阻力,求此时
(1)通过棒cd的电流Icd ;
(2)电动机对该装置的输出功率P;
(3)电动机转动角速度![]() 与弹簧伸长量x之间的函数关系.
与弹簧伸长量x之间的函数关系.
【答案】(1) ![]() ;(2)
;(2) ;(3)
;(3)![]()
【解析】(1)S断开时,cd棒静止,有
mg=kx0
S闭合时,cd棒静止,有
mg+B2Icdl=kx
联立解得Icd=![]()
(2)回路总电阻R总=R+![]() R=
R=![]() R
R
总电流I=2Icd=![]()
电动机对该装置的输出功率P=I2R总=
(3)由法拉第电磁感应定律得![]()
回路总电流![]()
联立解得ω=![]()

练习册系列答案
相关题目