题目内容
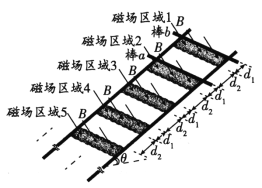
【题目】如图所示,间距为l的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计。磁感应强度均为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2。两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直。(设重力加速度为g)
(1)若导体棒a进入第2个磁场区域时,导体棒b以与a同样的速度进入第1个磁场区域,求导体棒b穿过第1个磁场区域过程中增加的动能△Ek;
(2)若导体棒a进入第2个磁场区域时,导体棒b恰好离开第1个磁场区域;此后导体棒a离开第2个磁场区域时,导体棒b又恰好进入第2个磁场区域,且导体棒a、b在任意一个磁场区域或无磁场区域的运动时间均相等。求导体棒a穿过第2个磁场区域过程中,通过导体棒a的电量q;
(3)对于第(2)问所述的运动情况,求导体棒a穿出第k个磁场区域时的速度v的大小。
【答案】(1)ΔEk=mgd1sinθ;(2)![]() ;(3)
;(3)![]()
【解析】
(1)a和b不受安培力的作用,由机械能守恒知
ΔEk=mgd1sinθ
(2)根据法拉第电磁感应定律有
![]()
根据闭合电路的欧姆定律有
![]()
又
![]() ,
,![]()
解得通过a棒的电量
![]()
(3)设导体棒刚进入无磁场区域时的速度为v1,刚离开无磁场区域时的速度为v2,在无磁场区域,根据牛顿第二定律有
mgsinθ=ma
根据运动学公式
v2-v1=at
![]()
有磁场区域,对a棒,根据动量定理
![]()
解得
v1=![]()
由题意知
v=v1=![]()

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目