��Ŀ����
15�� ��ͼ��ʾ����һ�̶������ڱڹ⻬�İ����棬����ΪO����͵�ΪC�������ڱ���������������Ϊm��С����Ϊ�ʵ㣩A��B���������߶Ȳ�ͬ��ˮƽ����������Բ���˶���A��Ĺ켣ƽ�����B��Ĺ켣ƽ�棬A��B������O�����������ֱ��OC��ļнǷֱ�Ϊ��=53��ͦ�=37�㣬����͵�C���ڵ�ˮƽ��Ϊ�������ܵIJο�ƽ�棬��sin37��=0.6��cos37��=0.8����������
��ͼ��ʾ����һ�̶������ڱڹ⻬�İ����棬����ΪO����͵�ΪC�������ڱ���������������Ϊm��С����Ϊ�ʵ㣩A��B���������߶Ȳ�ͬ��ˮƽ����������Բ���˶���A��Ĺ켣ƽ�����B��Ĺ켣ƽ�棬A��B������O�����������ֱ��OC��ļнǷֱ�Ϊ��=53��ͦ�=37�㣬����͵�C���ڵ�ˮƽ��Ϊ�������ܵIJο�ƽ�棬��sin37��=0.6��cos37��=0.8����������| A�� | A��B�������ܵ����Ĵ�С֮��Ϊ3��4 | B�� | A��B�����˶�������֮��Ϊ4��3 | ||
| C�� | A��B����Ķ���֮��Ϊ16��9 | D�� | A��B�������������֮��Ϊ2��1 |
���� С����������֧���������������ĺ����ṩ������������ƽ���ı��ζ������֧����֮�ȣ�����ţ�ٵڶ�����������ڡ����ٶ�֮�ȣ��Ӷ��ó�����֮�ȣ����ݸ߶�����������ܣ��Ӷ��ó���������֮�ȣ�
��� �⣺A������ƽ���ı��ζ���ã�С�����ܵĵ��� N=$\frac{mg}{cos��}$������С�����ڴ�����뾶����ֱ����ļнǣ���$\frac{{N}_{A}}{{N}_{B}}$=$\frac{cos��}{cos��}$=$\frac{cos37��}{cos53��}$=$\frac{4}{3}$����A����
B������mgtan��=mr$\frac{4{��}^{2}}{{T}^{2}}$��r=Rsin�ȣ�������� T=2��$\sqrt{\frac{Rcos��}{g}}$����$\frac{{T}_{A}}{{T}_{B}}$=$\sqrt{\frac{cos53��}{cos37��}}$=$\frac{\sqrt{3}}{2}$����B����
C����mgtan��=m$\frac{{v}^{2}}{r}$������ Ek=$\frac{1}{2}m{v}^{2}$����$\frac{1}{2}$mgRtan��sin�ȣ���A��B����Ķ���֮��$\frac{{E}_{KA}}{{E}_{KB}}$=$\frac{tan53��sin53��}{tan37��sin37��}$=$\frac{64}{27}$����C����
D��С�����������Ep=mgR��1-cos�ȣ�����A��B�������������֮��Ϊ$\frac{{E}_{PA}}{{E}_{PB}}$=$\frac{1-cos53��}{1-cos37��}$=2����D��ȷ��
��ѡ��D��
���� �������Ĺؼ���������������Դ������ţ�ٵڶ����ɵó����ٶȡ����ڵĹ�ϵ��

 ��ͼ��ʾ��뭡�뮡�밵�ԭ�Ӻ��Գ���Ϊ�㾭ͬһ�糡���ٺ��־�ͬһ��ǿ�糡ƫת��������ӫ�����ϣ���ô��������
��ͼ��ʾ��뭡�뮡�밵�ԭ�Ӻ��Գ���Ϊ�㾭ͬһ�糡���ٺ��־�ͬһ��ǿ�糡ƫת��������ӫ�����ϣ���ô��������| A�� | �������ٵ糡���̣�뭺����ܵĵ糡����� | |
| B�� | ����ƫת�糡���̣��糡����3�ֺ����Ĺ�һ���� | |
| C�� | 3��ԭ�Ӻ˴�������ʱ���ٶ�һ���� | |
| D�� | 3��ԭ�Ӻ˶��������ϵ�ͬһλ���� |
| A�� | ��Ȧ��һ���и�Ӧ���� | |
| B�� | ��Ȧ���и�Ӧ�綯�ƣ����С���ͨ�������� | |
| C�� | ��Ȧ���и�Ӧ�綯�ƣ����С���ͨ���ı仯�������� | |
| D�� | ��Ȧ��һ���и�Ӧ�綯�� |



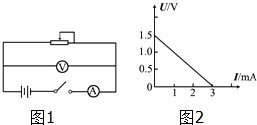 ������ˮ����ء��ĵ綯�ƺ��ڵ����ʵ���У���һͭƬ��һпƬ�ֱ����ͬһֻƻ���ڣ������˼ġ�ˮ����ء�����綯��ԼΪ1.5V���������ֵ�ز����ܵ������ѹΪ1.5V�������Ϊ0.3A���ֵ�Ͳ�ϵ�С���ݣ�ԭ��������С���ݵĵ���̫С�ˣ���ʵ��ⶨ����ԼΪ3mA�������������ģ�
������ˮ����ء��ĵ綯�ƺ��ڵ����ʵ���У���һͭƬ��һпƬ�ֱ����ͬһֻƻ���ڣ������˼ġ�ˮ����ء�����綯��ԼΪ1.5V���������ֵ�ز����ܵ������ѹΪ1.5V�������Ϊ0.3A���ֵ�Ͳ�ϵ�С���ݣ�ԭ��������С���ݵĵ���̫С�ˣ���ʵ��ⶨ����ԼΪ3mA�������������ģ� ����ƫ����3mA������Լ10��
����ƫ����3mA������Լ10�� ������0��1.5V������Լ1000��
������0��1.5V������Լ1000��


 ��ͼ��ʾ�������㹻���Ĺ⻬����ƽ�е��죬����ƽ����ˮƽ��ļн�Ϊ30�㣬�϶����ӵ���R=4�����ռ��д�ֱ�ڵ���ƽ�����ǿ�ų����Ÿ�Ӧǿ��B=1T��һ���뵼��Ӵ����õ�����m=0.2Kg������L=1m������r=1���Ľ�����MN�о�ֹ��ʼ�ص����»�������������ĵ�����Բ��ƣ�gȡ10m/s2��
��ͼ��ʾ�������㹻���Ĺ⻬����ƽ�е��죬����ƽ����ˮƽ��ļн�Ϊ30�㣬�϶����ӵ���R=4�����ռ��д�ֱ�ڵ���ƽ�����ǿ�ų����Ÿ�Ӧǿ��B=1T��һ���뵼��Ӵ����õ�����m=0.2Kg������L=1m������r=1���Ľ�����MN�о�ֹ��ʼ�ص����»�������������ĵ�����Բ��ƣ�gȡ10m/s2��