题目内容
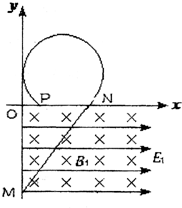 如图所示,在x轴下方存在着正交的电场与磁场,电场沿x轴正方向,电场强度E1=20N/C,磁场垂直纸面向里,磁感应强度B1=5T.一个质量m=3g,带电荷量q=2×10-3C的带电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m.在x轴上方存在正交的电场E2与磁场B2(图中均未画出),小球在x轴上方做圆周运动,恰好与y轴相切,运动轨迹如图所示.(g=10m/s2,sin37°=0.6),试求:?
如图所示,在x轴下方存在着正交的电场与磁场,电场沿x轴正方向,电场强度E1=20N/C,磁场垂直纸面向里,磁感应强度B1=5T.一个质量m=3g,带电荷量q=2×10-3C的带电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m.在x轴上方存在正交的电场E2与磁场B2(图中均未画出),小球在x轴上方做圆周运动,恰好与y轴相切,运动轨迹如图所示.(g=10m/s2,sin37°=0.6),试求:?(1)小球运动的速率v;?
(2)电场E2的大小与方向;?
(3)磁场B2的大小与方向.?
分析:(1)根据小球的运动可知小球受力平衡,合外力为零;对小球受力分析,利用力的合成与分解和共点力的平衡可求出速度的大小.
(2)由图可知,小球在x轴上方做匀速圆周运动,可判断受到的重力和电场力平衡,由二力平衡和可求出电场E2的大小和方向.
(3)小球在x轴上方做匀速圆周运动,由几何关系可求出轨道半径R为
m,向心力提供洛伦兹力,结合牛顿第二定律即可求出磁场B2的大小,由左手定则可判断方向.
(2)由图可知,小球在x轴上方做匀速圆周运动,可判断受到的重力和电场力平衡,由二力平衡和可求出电场E2的大小和方向.
(3)小球在x轴上方做匀速圆周运动,由几何关系可求出轨道半径R为
| 5 |
| 3 |
解答:解:
(1)小球从M向N做匀速直线运动,可知小球所受合外力为零,对小球受力分析(如图一所示),
受到重力、电场力和洛伦兹力作用,由小球的受力可知小球带正电,有:
tanθ=
=
=
∴θ=53°
洛伦兹力的大小与电场力和重力的合力大小相等,有:
qvB1=
得:v=5m/s
(2)小球x轴上方做匀速圆周运动(如图二所示),可知电场力与重力平衡,所以有: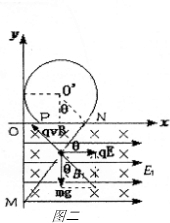
E2=
=
=15N/C
因小球带正电,所以E2方向沿y轴正方向.
(3)设小球在x轴上方做匀速圆周运动的半径为R,
由几何关系(如图二)可得:Rsin53°+R=ON
则:ON=OMtan37°
解得R=
m
小球做匀速圆周运动的向心力由洛伦兹力提供,由牛顿第二定律有:
qvB2=
得:B2=
=4.5T.
因小球带正电,由左手定则可知磁感应强度B2的方向垂直纸面向里.
答:(1)小球运动的速率为5m/s?
(2)电场E2的大小为15N/C,方向为沿y轴的正方向.?
(3)磁场B2的大小为4.5T,方向为垂直纸面向里.
(1)小球从M向N做匀速直线运动,可知小球所受合外力为零,对小球受力分析(如图一所示),
受到重力、电场力和洛伦兹力作用,由小球的受力可知小球带正电,有:

tanθ=
| qE1 |
| mg |
| 2×10-3×20 |
| 0.003×10 |
| 4 |
| 3 |
∴θ=53°
洛伦兹力的大小与电场力和重力的合力大小相等,有:
qvB1=
| mg |
| cos53° |
得:v=5m/s
(2)小球x轴上方做匀速圆周运动(如图二所示),可知电场力与重力平衡,所以有:

E2=
| mg |
| q |
| 0.003×10 |
| 2×10-3 |
因小球带正电,所以E2方向沿y轴正方向.
(3)设小球在x轴上方做匀速圆周运动的半径为R,
由几何关系(如图二)可得:Rsin53°+R=ON
则:ON=OMtan37°
解得R=
| 5 |
| 3 |
小球做匀速圆周运动的向心力由洛伦兹力提供,由牛顿第二定律有:
qvB2=
| mv2 |
| R |
得:B2=
| mv |
| qR |
因小球带正电,由左手定则可知磁感应强度B2的方向垂直纸面向里.
答:(1)小球运动的速率为5m/s?
(2)电场E2的大小为15N/C,方向为沿y轴的正方向.?
(3)磁场B2的大小为4.5T,方向为垂直纸面向里.
点评:该题考察了带电粒子在复合场中的运动.带电粒子在复合场中的运动情况有很多,常见的运动情况有如下几种:
1.带电粒子在复合场中所受的合外力为零时,粒子将处于静止状态或做匀速直线运动运动.
2.当带电粒子所受的合外力时刻指向一个圆心充当向心力时,粒子将做匀速圆周运动(如:电场力和重力相平衡,洛伦兹力提供向心力).
3.当带电粒子所受的合外力大小、方向均不断发生变化时,则粒子将非匀变速做曲线运动.
解决此类问题的关键是正确的对粒子进行受力分析和运动的分析,并结合草图进行解答.
1.带电粒子在复合场中所受的合外力为零时,粒子将处于静止状态或做匀速直线运动运动.
2.当带电粒子所受的合外力时刻指向一个圆心充当向心力时,粒子将做匀速圆周运动(如:电场力和重力相平衡,洛伦兹力提供向心力).
3.当带电粒子所受的合外力大小、方向均不断发生变化时,则粒子将非匀变速做曲线运动.
解决此类问题的关键是正确的对粒子进行受力分析和运动的分析,并结合草图进行解答.

练习册系列答案
相关题目
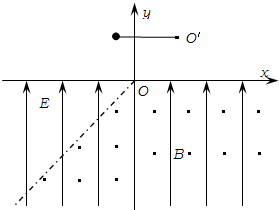 如图所示,在x轴下方有竖直向上的匀强电场其场强E=mg/q,在x轴下方的虚线(虚线与y轴成45° )右侧有垂直纸面向外的匀强磁场,磁感应强度为B.有一长为L的轻绳一端固定在第一象限内的O'点且可绕O'点在竖直平面内转动,另一端栓一质量为m的小球,小球电荷量为+q,OO'间距为L与x轴成45°,先将小球放在O'左边同一水平面上,使绳恰好伸直,让小球由静止释放,并设法使绳子在小球正好进入磁场的瞬间断开.求:
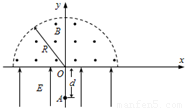
如图所示,在x轴下方有竖直向上的匀强电场其场强E=mg/q,在x轴下方的虚线(虚线与y轴成45° )右侧有垂直纸面向外的匀强磁场,磁感应强度为B.有一长为L的轻绳一端固定在第一象限内的O'点且可绕O'点在竖直平面内转动,另一端栓一质量为m的小球,小球电荷量为+q,OO'间距为L与x轴成45°,先将小球放在O'左边同一水平面上,使绳恰好伸直,让小球由静止释放,并设法使绳子在小球正好进入磁场的瞬间断开.求: (2013?汕头二模)如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B.y轴下方的A点与O点的距离为d.一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.不计粒子的重力作用.
(2013?汕头二模)如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B.y轴下方的A点与O点的距离为d.一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.不计粒子的重力作用.
 ,求粒子经过x轴时的位置.
,求粒子经过x轴时的位置.