题目内容
 (2013?汕头二模)如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B.y轴下方的A点与O点的距离为d.一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.不计粒子的重力作用.
(2013?汕头二模)如图所示,在x轴下方的区域内存在方向与y轴相同的匀强电场,电场强度为E.在x轴上方以原点O为圆心、半径为R的半圆形区域内存在匀强磁场,磁场的方向垂直于xy平面并指向纸面外,磁感应强度为B.y轴下方的A点与O点的距离为d.一质量为m、电荷量为q的带正电粒子从A点由静止释放,经电场加速后从O点射入磁场.不计粒子的重力作用.(1)求粒子在磁场中运动的轨道半径r.
(2)要使粒子进入磁场之后不再经过x轴,电场强度需大于或等于某个值E0.求E0.
(3)若电场强度E等于第(2)问E0的
| 2 | 3 |
分析:(1)带电粒子先在电场中加速后进入磁场中偏转.根据动能定理求加速获得的速度,由牛顿第二定律和向心力公式结合求磁场中运动的半径;
(2)要使粒子之后恰好不再经过x轴,则离开磁场时的速度方向与x轴平行,画出粒子的运动轨迹,由几何知识求出轨迹半径,由上题结论求E0.
(3)若电场强度E等于第(2)问E0的
,求粒子在磁场中运动的轨迹半径,画出粒子的运动轨迹,由几何知识求经过x轴时的位置.
(2)要使粒子之后恰好不再经过x轴,则离开磁场时的速度方向与x轴平行,画出粒子的运动轨迹,由几何知识求出轨迹半径,由上题结论求E0.
(3)若电场强度E等于第(2)问E0的
| 2 |
| 3 |
解答: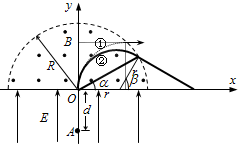 解:(1)粒子在电场中加速,由动能定理得qEd=
解:(1)粒子在电场中加速,由动能定理得qEd=
mv2 ①
粒子进入磁场后做圆周运动,有qvB=m
②
解得粒子在磁场中运动的半径 r=
③
(2)要使粒子之后恰好不再经过x轴,则离开磁场时的速度方向与x轴平行,运动情况如图①,由几何知识可得 R=
r ④
由以上各式解得 E0=
⑤
(3)将E=
E0代入可得磁场中运动的轨道半径 r=
⑥
粒子运动情况如图②,图中的角度α、β满足 cosα=
=
即α=30° ⑦
则得 β=2α=60° ⑧
所以 粒子经过x轴时的位置坐标为x=r+
⑨
解得x=
R ⑩
答:
(1)粒子在磁场中运动的轨道半径r为
.
(2)要使粒子进入磁场之后不再经过x轴,电场强度需大于或等于某个值E0.E0为
.
(3)若电场强度E等于第(2)问E0的
,粒子经过x轴时的位置为x=
R.
 解:(1)粒子在电场中加速,由动能定理得qEd=
解:(1)粒子在电场中加速,由动能定理得qEd=| 1 |
| 2 |
粒子进入磁场后做圆周运动,有qvB=m
| v2 |
| r |
解得粒子在磁场中运动的半径 r=
| ||
| qB |
(2)要使粒子之后恰好不再经过x轴,则离开磁场时的速度方向与x轴平行,运动情况如图①,由几何知识可得 R=
| 2 |
由以上各式解得 E0=
| qB2R2 |
| 4md |
(3)将E=
| 2 |
| 3 |
| R | ||
|
粒子运动情况如图②,图中的角度α、β满足 cosα=
| ||
| r |
| ||
| 2 |
则得 β=2α=60° ⑧
所以 粒子经过x轴时的位置坐标为x=r+
| r |
| cosβ |
解得x=
| 3 |
答:
(1)粒子在磁场中运动的轨道半径r为
| ||
| qB |
(2)要使粒子进入磁场之后不再经过x轴,电场强度需大于或等于某个值E0.E0为
| qB2R2 |
| 4md |
(3)若电场强度E等于第(2)问E0的
| 2 |
| 3 |
| 3 |
点评:本题是带电粒子在复合场中运动的类型,运用动能定理、牛顿第二定律和几何知识结合进行解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?汕头二模)某同学用如图1的装置验证机械能守恒定律.
(2013?汕头二模)某同学用如图1的装置验证机械能守恒定律. (2013?汕头二模)用显微镜观察墨汁液滴,追踪一个小炭粒的运动,每隔30s记录炭粒的位置并连线,记录的结果如图所示,下面表述正确的是( )
(2013?汕头二模)用显微镜观察墨汁液滴,追踪一个小炭粒的运动,每隔30s记录炭粒的位置并连线,记录的结果如图所示,下面表述正确的是( )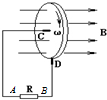 (2013?汕头二模)如图为圆盘发电机的示意图,铜盘绕水平的铜轴C在垂直于盘面的匀强磁场中转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( )
(2013?汕头二模)如图为圆盘发电机的示意图,铜盘绕水平的铜轴C在垂直于盘面的匀强磁场中转动,铜片D与铜盘的边缘接触,铜盘、导线和电阻R连接组成电路,则( ) (2013?汕头二模)如图,质量分别为ma和mb的两木块a、b之间有一轻弹簧被压缩,两木块在水平面上都保持静止,a、b所受的摩擦力分别Fa和Fb,下面表述正确的是( )
(2013?汕头二模)如图,质量分别为ma和mb的两木块a、b之间有一轻弹簧被压缩,两木块在水平面上都保持静止,a、b所受的摩擦力分别Fa和Fb,下面表述正确的是( )