题目内容
20. 如图所示,一个质量为m、电荷量为q的正电粒子,从静止进入一个电压为U1的加速电场后,又垂直进入一个电压为U2的偏转电场,偏转电场的两极板间距离为d,极板长为L.求:
如图所示,一个质量为m、电荷量为q的正电粒子,从静止进入一个电压为U1的加速电场后,又垂直进入一个电压为U2的偏转电场,偏转电场的两极板间距离为d,极板长为L.求:(1)正粒子射入偏转电场时的速度;
(2)正粒子在偏转电场时的加速度;
(3)粒子飞出偏转电场时的侧移距离;
(4)粒子飞出偏转电场时的偏转角的正切值.
分析 (1)带电粒子在加速电场中电场力做正功,由动能定理可解速度出加速电场时的速度υ.
(2)根据牛顿运动定律求解加速度;
(3)带电粒子在偏转电场中做类平抛运动,利用运动的合成与分解的观点解决偏转量y.
解答 解:(1)在加速电场运动过程中,由动能定理:qU1=$\frac{1}{2}$mv2
得v=$\sqrt{\frac{2q{U}_{1}}{m}}$
(2)带电粒子在偏转电场中的加速度:a=$\frac{qE}{m}$
E=$\frac{{U}_{2}}{d}$
所以:a=$\frac{q{U}_{2}}{md}$
(3)带电粒子在偏转电场的运动时间:t=$\frac{L}{v}$
带电粒子离开电场时的偏转量:y=$\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{q{U}_{2}}{md}•\frac{{L}^{2}}{{v}^{2}}=\frac{{U}_{2}{L}^{2}}{4d{U}_{1}}$
(4)粒子射出电场时,沿电场线方向的分速度:${v}_{y}=at=\frac{q{U}_{2}}{md}•\frac{L}{v}$
粒子飞出偏转电场时的偏转角的正切值:tanθ=$\frac{{v}_{y}}{v}=\frac{q{U}_{2}L}{md{v}^{2}}=\frac{{U}_{2}L}{2d{U}_{1}}$
答:(1)正粒子射入偏转电场时的速度是$\sqrt{\frac{2q{U}_{1}}{m}}$;
(2)正粒子在偏转电场时的加速度是 $\frac{q{U}_{2}}{md}$;
(3)粒子飞出偏转电场时的侧移距离是$\frac{{U}_{2}{L}^{2}}{4d{U}_{1}}$;
(4)粒子飞出偏转电场时的偏转角的正切值是$\frac{{U}_{2}L}{2d{U}_{1}}$.
点评 该题考查带电粒子在电场中的加速与粒子在电场中的偏转,对单个粒子的加速运用动能定理很简便,利用运动的合成与分解的观点解决类平抛问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,质量相同且分布均匀的两个圆柱体a、b靠在一起,表面光滑,重力均为G,其中b的下一半刚好固定在水平面MN的下方,上边露出另一半,a静止在平面上,现过a的轴心施以水平作用力F,缓慢的将a拉离平面一直滑到b的顶端,对圆柱体a的移动过程分析,应有( )
如图所示,质量相同且分布均匀的两个圆柱体a、b靠在一起,表面光滑,重力均为G,其中b的下一半刚好固定在水平面MN的下方,上边露出另一半,a静止在平面上,现过a的轴心施以水平作用力F,缓慢的将a拉离平面一直滑到b的顶端,对圆柱体a的移动过程分析,应有( )| A. | 开始时拉力F最大为G | B. | 拉力F先增大后减小 | ||
| C. | a、b间压力由0逐渐增大 | D. | a、b间的压力开始最大为2G |
| A. | 它是竖直向下的初速度为0,加速度为g的匀加速直线运动 | |
| B. | 在开始连续的三个2s内通过的位移之比为1:3:5 | |
| C. | 在开始连续的三个2s末的速度大小为1:2:3 | |
| D. | 从开始运动依次下落的三段位移,每段所经历的时间之比为1:$\sqrt{2}$:$\sqrt{3}$ |
| A. | 在地球上不同的地方,一切物体做自由落体的加速度都相同 | |
| B. | 在地面上不同的地方,g的大小不同 | |
| C. | 重力加速度g是矢量,方向竖直向下 | |
| D. | 在地球上的同一地方,离地面高度越大,重力加速度越大 |
 如图所示为某同学测物块与斜面间的动摩擦因数的实验装置,在斜面BC的底端垂直放一光电计时器,将物块放置在斜面的顶端,在物块上固定挡光片,已知挡光片的宽度为d,让物块在斜面顶端由静止释放,记录挡光片通过光电计时器的时间为△t.
如图所示为某同学测物块与斜面间的动摩擦因数的实验装置,在斜面BC的底端垂直放一光电计时器,将物块放置在斜面的顶端,在物块上固定挡光片,已知挡光片的宽度为d,让物块在斜面顶端由静止释放,记录挡光片通过光电计时器的时间为△t.
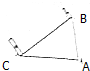
 如图所示,在水平向右的匀强电场中,一长为L的细线拴一质量为m带电量为+q的小球,小球不运动时停在B处,B处细线与竖直方向成37°,当地重力加速度为g,空气阻力不计.现将小球拉到最低位置A点由静止释放(Sin37°=0.6,cos37°=0.8).求:
如图所示,在水平向右的匀强电场中,一长为L的细线拴一质量为m带电量为+q的小球,小球不运动时停在B处,B处细线与竖直方向成37°,当地重力加速度为g,空气阻力不计.现将小球拉到最低位置A点由静止释放(Sin37°=0.6,cos37°=0.8).求: