题目内容
如图1所示，质量m=1kg的物体放在倾角为θ的斜面上，斜面体质量M=2kg，斜面与物体间的动摩擦因数μ=0．2，地面光滑，θ=37°.现对斜面体施以水平推力F，要使物体m相对斜面静止，力F应为多大？（设物体与斜面间的最大静摩擦力等于滑动摩擦力，g=10m/s2，sin37°=0.6，cos37°=0.8）
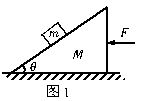
见试题分析
【试题分析】
本题中若推力F过小，则m相对于M有向下运动的趋势，静摩擦力应向上.假设推力F=F1时，m恰好静止在M上.则对（M+m）整体用牛顿第二定律有
F1=（M+m）a1
隔离m，对其进行受力分析，受力图如图2所示.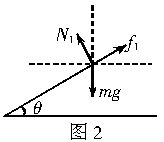
对m用牛顿第二定律有
N1sinθ-f1cosθ=ma1
竖直方向由平衡条件有
N1cosθ+f1sinθ=mg
又 f1=μN1
解得a1=4.78m/s2，F1=14.34N
当推力F过大时，物体相对于斜面有向上运动的趋势，此时的静摩擦力应沿斜面向下.假设F=F2时，m恰好静止在M上.则对（M+m）整体用牛顿第二定律有
F2=（M+m）a2
隔离m，对其画受力图，如图3所示.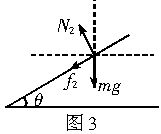
则有
N2sinθ+2cosθ=ma2 N2cosθ-f2sinθ=mg
f2=μN2
解得 a2=11.18m/s2，F2=33.54N
故 14.34N≤F≤33.54N
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
0.6，cos37°=0.8g=10m/s2）求：