题目内容
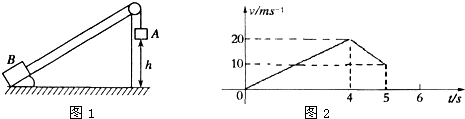
如图1所示,质量m=1kg的物体B置于倾角θ=37°的固定斜面上,用轻绳通过光滑的滑轮与物体A相连.t=0时同时释放A、B,物体A拉动B沿斜面向上运动,已知斜面足够长,A落地后不再反弹,物体B运动的部分v-t图如图2所示,求:

(1)物体A的质量;
(2)物体B在上升过程中,和斜面摩擦产生的热量;
(3)若物体B到达最高点时,剪断绳子.取地面为零势能参考平面,物体B向下滑动过程中在何位置时具有的动能和势能相等.

(1)物体A的质量;
(2)物体B在上升过程中,和斜面摩擦产生的热量;
(3)若物体B到达最高点时,剪断绳子.取地面为零势能参考平面,物体B向下滑动过程中在何位置时具有的动能和势能相等.
分析:(1)根据速度时间图线求出匀加速和匀减速直线运动的加速度大小,结合牛顿第二定律对两个过程列式,可求出动摩擦因数的大小和A的质量.
(2)根据速度图象的“面积”求出B向上滑行的距离,即可求得摩擦产生的热量.
(3)根据动能定理和动能和势能相等的条件列式,即可求得B下滑的高度.
(2)根据速度图象的“面积”求出B向上滑行的距离,即可求得摩擦产生的热量.
(3)根据动能定理和动能和势能相等的条件列式,即可求得B下滑的高度.
解答:解:(1)速度时间图线的斜率等于加速度,则得:匀加速和匀减速直线运动的加速度大小分别为:
a1=
=
m/s2=5m/s2;
a2=
=
m/s2=10m/s2;
由图看出,t=4s时刻A落地,对匀加速和匀减速运动两个过程,根据牛顿第二定律得:
mAg-mBgsinθ-μmBgcosθ=(mA+mB)a1;
mBgsinθ+μmBgcosθ=mBa2;
代入解得,mA=3kg,
μ=0.5;
(2)根据速度图象的“面积”等于位移大小,可得:
匀加速运动的位移为 x1=
×4×20m=40m
减速阶段通过的位移为x2=
=
m=20m
总位移为x=x1+x2=60m;
摩擦产生的热量Q=μmBgcos37°×x1=0.5×1×10×0.8×60J=240J;
(3)设距地面的高度为h,则下滑的高度为H=xsin37°-h=36-h,
沿斜面通过的位移为x′=
=60-
h
由动能定理可得
mgH-μmgcos37°?x′=EK
EP=mgh
EK=Ep
联立解得h=7.5m;
答:(1)物体A的质量为3kg.
(2)物体B在上升过程中,和斜面摩擦产生的热量为240J.
(3)物体B向下滑动过程中距离地面7.5m高的位置时具有的动能和势能相等.
a1=
| △v |
| △t |
| 20 |
| 4 |
a2=
| △v |
| △t |
| 20-10 |
| 1 |
由图看出,t=4s时刻A落地,对匀加速和匀减速运动两个过程,根据牛顿第二定律得:
mAg-mBgsinθ-μmBgcosθ=(mA+mB)a1;
mBgsinθ+μmBgcosθ=mBa2;
代入解得,mA=3kg,
μ=0.5;
(2)根据速度图象的“面积”等于位移大小,可得:
匀加速运动的位移为 x1=
| 1 |
| 2 |
减速阶段通过的位移为x2=
| v2 |
| 2a2 |
| 202 |
| 2×10 |
总位移为x=x1+x2=60m;
摩擦产生的热量Q=μmBgcos37°×x1=0.5×1×10×0.8×60J=240J;
(3)设距地面的高度为h,则下滑的高度为H=xsin37°-h=36-h,
沿斜面通过的位移为x′=
| H |
| sin37° |
| 5 |
| 3 |
由动能定理可得
mgH-μmgcos37°?x′=EK
EP=mgh
EK=Ep
联立解得h=7.5m;
答:(1)物体A的质量为3kg.
(2)物体B在上升过程中,和斜面摩擦产生的热量为240J.
(3)物体B向下滑动过程中距离地面7.5m高的位置时具有的动能和势能相等.
点评:本题主要考查了牛顿第二定律和动能定理的应用,要求同学们能正确对物体进行受力分析,注意整体法和隔离法的应用.

练习册系列答案
相关题目



 0.6,cos37°=0.8g=10m/s2)求:
0.6,cos37°=0.8g=10m/s2)求: