题目内容
（20）导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示，固定于水平面的U形导线框处于竖直向下的匀强磁场中，金属直导线MN在与其垂直的水平恒力F的作用下，在导线框上以速度v做匀速运动，速度v与恒力F方向相同，导线MN始终与导线框形成闭合电路，已知导线MN电阻为R，其长度L，恰好等于平行轨道间距，磁场的磁感应强度为B，忽略摩擦阻力和导线框的电阻。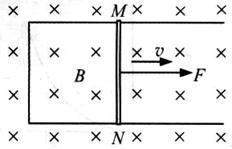
（1）通过公式推导验证：在时间内
，F对导线MN所做的功W等于电路获得的电能
，也等于导线MN中产生的焦耳热Q。
（2）若导线的质量m=8.0g，长度L=0.1m，感应电流I=1.0A，假设一个原子贡献1个自由电子，计算导线MN中电子沿导线长度方向定向移动的平均速率v（下表中列出了一些你可能用到的数据）。
（3）经典物理学认为，金属的电阻源于定向运动自由电子和金属离子（金属原子失去电子后剩余部分）的碰撞，展开你想象的翅膀，给出一个合理的自由电子运动模型：在此基础上，求出导线MN中金属离子对一个自由电子沿导线长度方向的平均作用力
的表达式。
（1）见解析（2）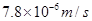 
（3） 
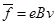
解析试题分析：
（1）导线运动时产生的感应电动势为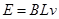
，
导线中的电流为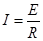
，
导线受到的安培力为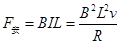
，
物体匀速运动，拉力和安培力相等，所以拉力为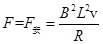
，
拉力F做功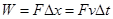
，将F代入得到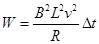
电能为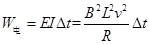
，
产生的焦耳热为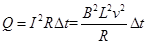
，由此可见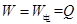
（2）导线MN中的总电子数N=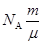
，
导线MN中电子的电量为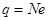
通过导线的电流为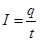
这些电量通过导线横截面积的时间为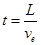
联立以上各式得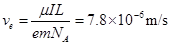
（3）方法一：动量解法
设电子在每一次碰撞结束至下一次碰撞结束之间的运动都相同，设经历的时间为，电子的动量变化为零。
因为导线MN的运动，电子受到沿导线方向的洛伦兹力为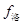
的作用，有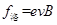
沿导线方向，电子只受到金属离子的作用力和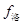作用，所以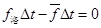
联立解得电子受到的平均作用力为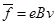
方法二：能量解法
设电子从导线的一端到达另一端经历的时间为t，在这段时间内，通过导线一端的电子总数为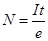
电阻上产生的焦耳热是由于克服金属离子对电子的平均作用力做功而产生的，有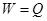
在t时间内电子运动过程中克服阻力所做的功，可以表示为
电流产生的焦耳热为：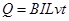
联立解得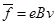
考点：电磁感应、能量守恒定律的综合考查
a、b是竖直方向上同一电场线上的两点，一带负电的质点在a点由静止释放，到达b点时速度最大，则
| A．a点电势高于b点电势 |
| B．a点的场强大于b点场强 |
| C．质点从a点运动到b点的过程中电势能增加 |
| D．质点在a点受到的电场力小于在b点受到的电场力 |
，此区域外导轨是光滑的。电动小车沿PS以v=1.0m/s的速度匀速前进时，滑杆经d=1m的位移由AA’滑到OO’位置。（g取10m/s2）求：
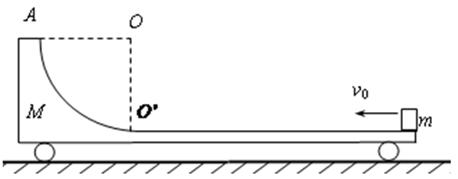
点相切．现将一质量m =" 1.0" kg的小物块（可视为质点）从平板车的右端以水平向左的初速度v0滑上平板车，小物块与水平轨道间的动摩擦因数
，小物块恰能到达圆弧轨道的最高点A．取g =" 10" m/s2，求：
