题目内容

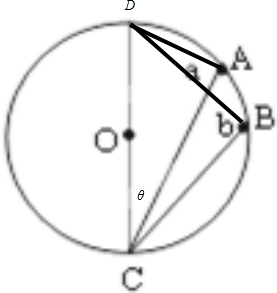
如图所示，AC、BC为位于竖直平面内的两根光滑细杆，A、B、C三点恰位于同一圆周上，C为该圆周的最低点，a、b为套在细杆上的两个小环，当两环同时从A、B点自静止开始下滑，则 （　　）
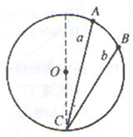
A．a环将先到达C点
B．b环将先到达C点
C．a、b环同时到达C点
D．由于两杆的倾角不知道，无法判断两环到达c点的先后

小环在杆上做初速度为0的匀加速直线运动，如图，∠ACD=θ，小环在杆上下滑时的加速度a=gcosθ，令圆的半径为R，则根据几何关系有：
AC=2Rcosθ
小环在AC上下滑的加速度a=gcosθ，因为小环做初速度为0的匀加速直线运动，根据位移时间关系有：
AC=
1
2
at2
即2Rcosθ=
1
2
gcosθt2，
解得：t=
4R
g
，与杆的倾角θ无关，故C正确，ABD错误．
故选：C．
练习册系列答案
相关题目
如图所示，长L=9m的传送带与水平方向的傾角θ=37°，在电动机的带动下以υ=4m/s的速率顺时针方向运行，在传送带的B端有一离传送带很近的挡板P可将传送带上的物块挡住，在传送带的A端无初速地放一质量m=1kg的物块，它与传送带间的动摩擦因数μ=0.5，物块与挡板的碰撞能量损失及碰撞时间不计．（g=10m/s2，sin37°=0.6）求：
（1）物块从第一次静止释放到与挡板P第一次碰撞后，物块再次上升到传送带的最高点的过程中，因摩擦生的热；
（2）物块最终的运动状态及达到该运动状态后电动机的输出功率．
如图甲所示，某人正通过定滑轮将质量为m的货物提升到高处，滑轮的质量和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示．g表示当地的重力加速度大小，由图可以判断（　　）
A．图象与纵轴的交点M的值aM=g
B．图象与横轴的交点N的值TN=mg
C．图象的斜率等于物体的质量m
D．图象的斜率等于物体质量的倒数
1
m
如图所示，一块质量为M=2kg，长L=lm的匀质木板放在足够长的水平桌面上，初始时速度为零．板的最左端放置一个质量m=lkg的小物块，小物块与木板间的动摩擦因数为μ1=0.2，小物块上连接一根足够长的水平轻质细绳，细绳跨过位于桌面边缘的定滑轮（细绳与滑轮间的摩擦不计，木板与滑轮之间距离足够长，g=10m/s2），要求：
（1）若木板被固定，恒力F=4N向下拉绳，求小木块滑离木板时的速度大小v1；
（2）若不固定木板，且板与桌面间光滑，某人仍以恒力F=4N向下拉绳，求小木块滑离木板时的速度大小v2；
（3）若不固定木板，若板与桌面间有摩擦，某人以恒定速度v=1m/s向下拉绳，为使物块能从板的右端滑出，求板与桌面间的动摩擦因数μ2．
质量为4.0×103kg的汽车，在4.8×103N的水平恒力牵引下，从静止开始沿水平道路做匀加速直线运动，经过10s前进40m，求：
（1）汽车加速度的大小；
（2）汽车所受阻力的大小．
如图所示，自由下落的小球，从它接触竖直放置的弹簧开始，到弹簧被压缩到最短的过程中，小球的速度和所受外力的合力变化情况是（　　）
A．合力变小，速度变小
B．合力变小，速度变大
C．合力先变小后变大，速度先变大后变小
D．合力先变大后变小，速度先变小后变大
如图所示，两半径为60cm的转盘固定在间距可以调整的竖直平面上，转盘固在电动机带动下均以5rad/s的角速度向相反方向转动．在竖直方向上一有质量为2kg，长为2m的直杆，其顶端刚好被两转盘夹住．现直杆从静止开始在转盘作用下向上运动，已知直杆与转盘间的动摩擦因数μ=0.1，两转盘分别对木杆两侧的垂直压力为110N，g=10m/s2．求：
（1）转盘边缘的线速度；
（2）直杆向上穿过转盘的时间．
一辆汽车正在以c=20m/s的速度在平直路面匀速行驶，突然，司机看见车的正前方，处有一位静止站立的老人，司机立即采取制动措施．此过程汽车运动的速率随时间的变化规律如图所示，g取10m/s2，求：
（1）s至少多大时，老人是安全的；（设老人在整个过程都静止不动）
（2）汽车与地面的动摩擦因数．（刹车过程空气阻力不计）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网