题目内容
如图甲所示，某人正通过定滑轮将质量为m的货物提升到高处，滑轮的质量和摩擦均不计，货物获得的加速度a与绳子对货物竖直向上的拉力T之间的函数关系如图乙所示．g表示当地的重力加速度大小，由图可以判断（ ）
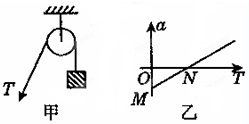
| A．图象与纵轴的交点M的值aM=g | ||
| B．图象与横轴的交点N的值TN=mg | ||
| C．图象的斜率等于物体的质量m | ||
D．图象的斜率等于物体质量的倒数
|
对货物受力分析，受重力mg和拉力T，根据牛顿第二定律，有
T-mg=ma，得 a=
-g
A、当T=0时，a=-g，即图线与纵轴的交点M的值aM=-g，故A错误；
B、当a=0时，T=mg，故图线与横轴的交点N的值TN=mg，故B正确；
C、D图线的斜率表示质量的倒数
，故C错误，D正确；
故选BD．
T-mg=ma，得 a=
| T |
| m |
A、当T=0时，a=-g，即图线与纵轴的交点M的值aM=-g，故A错误；
B、当a=0时，T=mg，故图线与横轴的交点N的值TN=mg，故B正确；
C、D图线的斜率表示质量的倒数
| 1 |
| m |
故选BD．
练习册系列答案
阅读快车系列答案
相关题目
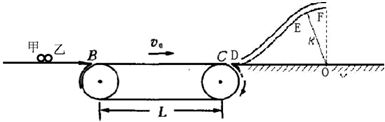点，乙小球离开传送带时与传送带速度相等，从D处进入细管到达细管的最高点F水平飞出，求：
