题目内容
【题目】如图所示，一球A夹在竖直墙与三角形劈B的斜面之间．三角形劈的重力为G，劈的底部与地面之间的动摩擦因数为μ，劈的斜面与竖直墙面是光滑的，劈的斜面倾角为45°．问：欲使劈静止不动，球的重力不能超过多大？（设劈的最大静摩擦力等于滑动摩擦力）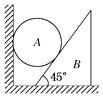
【答案】解：球A和劈B受力如下图，
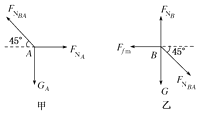
对球A，GA=FNBAsin45°，
对劈B，Ffm=FNBAcos45°，FNB=G+FNBAsin45°，
又有Ffm=μFNB，
联立解得GA= 
G．
答：球的重力不能超过 G．
【解析】分别画出A和B的受力示意图，对球A竖直方向根据共点力的平衡条件列方程，对劈B竖直方向和水平方向根据共点力的平衡条件列方程，联立求解．
【考点精析】根据题目的已知条件，利用静摩擦力和力的分解的相关知识可以得到问题的答案，需要掌握静摩擦力:静摩擦力大小可在0与fmax 之间变化，一般应根据物体的运动状态由平衡条件或牛顿定律来求解；求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法．
练习册系列答案
相关题目
