题目内容
如图所示,1为同步卫星,2为近地卫星,3为赤道上的一个物体,它们都在同一平面内绕地心做圆周运动.关于它们的圆周运动的线速度、角速度、和向心加速度,下列说法正确的是( )
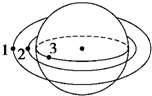
| A.v2=v3>v1 | B.ω1=ω3<ω2? | C.a1<a2=a3 | D.a2>a1>a3 |

A、物体3和同步卫星1周期相等,则角速度相等,
即ω1=ω3,根据v=rω,
则v1>v3,
卫星2和卫星1都靠万有引力提供向心力,根据
=
,
解得v=
,知轨道半径越大,线速度越小,则v2>v1.所以v2>v1>v3,故A错误;
B、物体3和同步卫星1周期相等,则角速度相等,即ω1=ω3,
根据ω=
,知轨道半径越大,角速度越小,则ω2>ω1.所以ω1=ω3<ω2?,故B正确;
C、物体3和同步卫星1周期相等,则角速度相等,即ω1=ω3,而加速度a=rω2,
则a1>a3,
卫星2和卫星1都靠万有引力提供向心力,根据
=ma,
a=
,知轨道半径越大,角速度越小,向心加速度越小,则a2>a1,
所以a2>a1>a3,故C错误,D正确;
故选:BD.
即ω1=ω3,根据v=rω,
则v1>v3,
卫星2和卫星1都靠万有引力提供向心力,根据
| GMm |
| r2 |
| mv2 |
| r |
解得v=
|
B、物体3和同步卫星1周期相等,则角速度相等,即ω1=ω3,
根据ω=
|
C、物体3和同步卫星1周期相等,则角速度相等,即ω1=ω3,而加速度a=rω2,
则a1>a3,
卫星2和卫星1都靠万有引力提供向心力,根据
| GMm |
| r2 |
a=
| GM |
| r2 |
所以a2>a1>a3,故C错误,D正确;
故选:BD.

练习册系列答案
相关题目
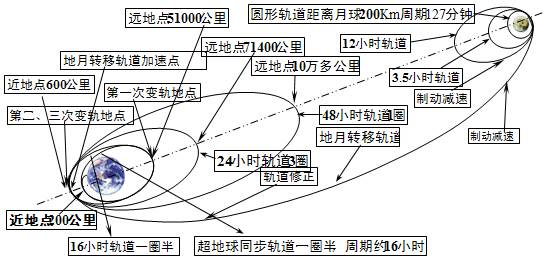
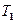 近似当作2小时,请根据图中数据计算出卫星在12小时轨道运行时,远月点与月球表面的距离。
近似当作2小时,请根据图中数据计算出卫星在12小时轨道运行时,远月点与月球表面的距离。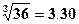 ,计算结果保留2位有效数字)
,计算结果保留2位有效数字)
