题目内容
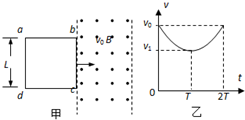
如图甲所示,光滑绝缘水平面上一矩形金属线圈abcd的质量为m、电阻为R、ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为v1,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.
(1)求t=0时刻线圈的电功率;
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为多少?
(3)若线圈的面积为S,请运用牛顿第二运动定律和电磁学规律证明:在线圈进人磁场过程中v0-v1=
.
(1)求t=0时刻线圈的电功率;
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为多少?
(3)若线圈的面积为S,请运用牛顿第二运动定律和电磁学规律证明:在线圈进人磁场过程中v0-v1=
| B2LS |
| mR |

(1)t=0时,E=BLv0
线圈电功率P=
=
(2)线圈进入磁场的过程中动能转化为焦耳热
Q=
mv02-
mv12
外力做功一是增加动能,二是克服安培力做功
WF=△Ek+Q=mv02-mv12
(3)根据微元法思想,将时间分为若干等分,每一等分可看成匀变速
vn-vn+1=
tn
∴v0-v1=
(I1t1+I2t2+…+Intn)
其中I1t1+I2t2+…+Intn=Q
电量Q=It=
=
∴v0-v1=
答:
(1)t=0时刻线圈的电功率是
;
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为
mv02-
mv12和mv02-mv12.
(3)证明略.
线圈电功率P=
| E2 |
| R |
| B2L2v02 |
| R |
(2)线圈进入磁场的过程中动能转化为焦耳热
Q=
| 1 |
| 2 |
| 1 |
| 2 |
外力做功一是增加动能,二是克服安培力做功
WF=△Ek+Q=mv02-mv12
(3)根据微元法思想,将时间分为若干等分,每一等分可看成匀变速
vn-vn+1=
| BLIn |
| m |
∴v0-v1=
| BL |
| m |
其中I1t1+I2t2+…+Intn=Q
电量Q=It=
| △φ |
| R |
| BS |
| R |
∴v0-v1=
| B2LS |
| mR |
答:
(1)t=0时刻线圈的电功率是
| B2L2v02 |
| R |
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为
| 1 |
| 2 |
| 1 |
| 2 |
(3)证明略.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,线圈中感应电流I随时间t变化的图象如图乙所示.求:
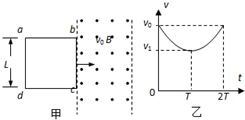
中,线圈中感应电流I随时间t变化的图象如图乙所示.求: (2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )
(2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )