题目内容
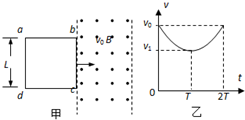
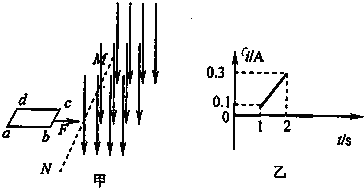
如图甲所示,光滑绝缘水平面上,磁感应强度B=2T的匀强磁场以虚线MN为左边界,MN的左侧有一质量m=0.1kg,bc边长L1=0.2m,电阻R=2Ω的矩形线圈abcd.t=0时,用一恒定拉力F拉线圈,使其由静止开始向右做匀加速运动,经过时间1s,线圈的bc边到达磁场边界MN,此时立即将拉力F改为变力,又经过1s,线圈恰好完全进入磁场.整个运动过程中,线圈中感应电流i随时间t变化的图象如图乙所示.
(1)求线圈bc边刚进入磁场时的速度v1和线圈在第ls内运动的距离x;
(2)写出第2s内变力F随时间t变化的关系式;
(3)求出线圈ab边的长度L2.
(1)求线圈bc边刚进入磁场时的速度v1和线圈在第ls内运动的距离x;
(2)写出第2s内变力F随时间t变化的关系式;
(3)求出线圈ab边的长度L2.

分析:(1)由图乙所示图象读出感应电流,由欧姆定律求感应电动势,由E=BLv求出线圈的速度;由匀变速运动的位移公式求出位移x.
(2)根据法拉第电磁感应定律和欧姆定律得出安培力与时间的关系式,由运动学公式求出加速度,再根据牛顿第二定律得到拉力与时间的关系式.
(3)先求出2s末的速度,利用平均速度公式求ab长度.
(2)根据法拉第电磁感应定律和欧姆定律得出安培力与时间的关系式,由运动学公式求出加速度,再根据牛顿第二定律得到拉力与时间的关系式.
(3)先求出2s末的速度,利用平均速度公式求ab长度.
解答:解:(1)由图乙可知,线圈刚进入磁场时的感应电流 I1=0.1A,
由 E=BLv1 及 I=
得 ①
v1=
=
m/s=0.5m/s ②
第1s内运动的距离 x=
t=
×1m=0.25m ③
(2)由图乙可知,在第2s时间内,线圈中的电流随时间均增加,线圈速度随时间均匀增加,线圈所受安培力随时间均匀增加,且大小F安=BIL1=(0.08t-0.04)N ④
t=2s时线圈速度 v2=
=1.5m/s ⑤
线圈在第2s时间内的加速度 a2=
=
m/s2=1m/s2 ⑥
由牛顿定律得F=F安+ma=(0.08t+0.06)N ⑦
(3)在第2s时间内,线圈的平均速度
=
=
m/s=1m/s ⑧
L2=
?t=1×1m=1m ⑨
答:(1)线圈bc边刚进入磁场时的速度v1为0.5m/s,线圈在第ls内运动的距离x为0.25m;(2)第2s内变力F随时间t变化的关系式为F=(0.08t+0.06)N;
(3)线圈ab边的长度L2为1m.
由 E=BLv1 及 I=
| E |
| R |
v1=
| I1R |
| BL1 |
| 0.1×2 |
| 2×0.2 |
第1s内运动的距离 x=
| v1 |
| 2 |
| 0.5 |
| 2 |
(2)由图乙可知,在第2s时间内,线圈中的电流随时间均增加,线圈速度随时间均匀增加,线圈所受安培力随时间均匀增加,且大小F安=BIL1=(0.08t-0.04)N ④
t=2s时线圈速度 v2=
| I2R |
| BL1 |
线圈在第2s时间内的加速度 a2=
| v2-v1 |
| t |
| 1.5-0.5 |
| 1 |
由牛顿定律得F=F安+ma=(0.08t+0.06)N ⑦
(3)在第2s时间内,线圈的平均速度
. |
| v |
| v1+v2 |
| 2 |
| 1.5+0.5 |
| 2 |
L2=
. |
| v |
答:(1)线圈bc边刚进入磁场时的速度v1为0.5m/s,线圈在第ls内运动的距离x为0.25m;(2)第2s内变力F随时间t变化的关系式为F=(0.08t+0.06)N;
(3)线圈ab边的长度L2为1m.
点评:本题分析和计算安培力和拉力是关键,根据安培力的方向判断线圈的运动情况,要熟练地根据法拉第定律、欧姆定律等等规律推导安培力的表达式.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
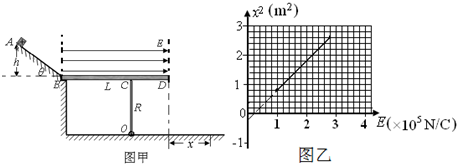
 中,线圈中感应电流I随时间t变化的图象如图乙所示.求:
中,线圈中感应电流I随时间t变化的图象如图乙所示.求: (2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )
(2011?崇明县二模)如图甲所示,光滑绝缘的水平面上一矩形金属线圈 abcd的质量为m、电阻为R、面积为S,ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为vl,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.则下列各项正确的是( )