题目内容
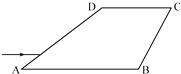
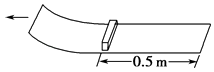
【题目】如图所示,质量M=4kg的木板静置于光滑水平面上,质量m=1kg的小物块(可视为质点)以初速度v0=4m/s从木板的左端冲上木板,同时在木板的右端施加一个水平向右F=2N的恒力,经t=1s撤去外力,最后小物块恰好不从木板的上端滑下,已知小物块与木板之间的动摩擦因数μ=0.2,重力加速度g=10m/s2 , 求:
(1)经过t=1s,小物块在木板上滑动的距离△x1为多少?
(2)木板的长度l为多少?
【答案】
(1)解:物块所受摩擦力f=μmg=2N,根据牛顿第二定律得:a= ![]() ,
,
t=1s时木块的速度为:v=at=2m/s,
木块运动的位移为:s= ![]()
木板所受合外力为:F合=F+f=4N,
所以加速度为:a2= ![]() =1m/s2,
=1m/s2,
木板运动的位移为:x= ![]()
所以有:△x1=s﹣x=2.5m
答:经过t=1s,小物块在木板上滑动的距离△x1为2.5m;
(2)解:撤去外力时,物块的速度是2m/s,木板的速度v2=a2t=1m/s,小物块恰好不从木板的上端滑下,则末速度相等,根据动量守恒定律得:
mv+Mv2=(m+M)v1
解得:v1=1.2m/s
对整个系统根据动能定理得:
![]()
解得:x1=0.2m
则木板的长度为:l=△x+x1=2.7m
答:木板的长度l为2.7m.
【解析】本题主要考查动量守恒定律的有关知识,涉及两个物体的动力学问题,分析清楚两个物体之间的关系,知道在过程中,两个物体组成的系统动量守恒。
【考点精析】关于本题考查的动量守恒定律,需要了解动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变才能得出正确答案.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目