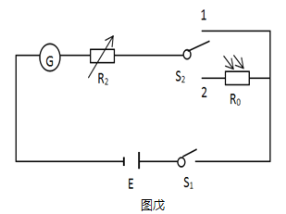
��Ŀ����
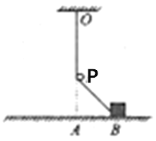
����Ŀ����ͼ��ʾ�����Ϊ30�����㹻��б��̶���ˮƽ���ϣ��Ử�ֵĶ�����̶�����ֱƽ����Բ����Բ��O��Բ���ϵ�P����ͬһˮƽ���ϣ�ϸ��һ�������ڻ�������Ϊm��С����������һ�˿������������ΪM���������������ֱ��������������С��ֹ��Q�㣬ϸ���뻷ǡ�����У�OQ��OP���53���ǡ���ȥ���������˶���P���ٶ�ǡ��Ϊ�㡣����һ��Ħ�����������ٶ�Ϊg��ȡsin53����0.8��cos53����0.6����
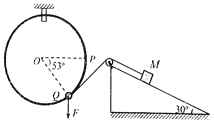
(1)�����Ĵ�СF��
(2)�����������֮��![]() ��
��
(3)�������˶���Q��ʱ��ϸ������T�Ĵ�С��
���𰸡���1��![]() ��2��M��m��12��5��3��
��2��M��m��12��5��3��![]()
��������
��1������ƽ����������M��m�ֱ��г�ƽ�ⷽ�̼��ɣ�
��2����M��m�г�ϵͳ��е���غ㣬������⣻
��3����M��m����ţ�ٵڶ������г����̼��ɣ�
��1����ϸ�ߵ�����Ϊ![]() ������ƽ���������Եõ���
������ƽ���������Եõ���
���M��![]()
��m��![]()
�õ���![]() ��
��
��2���軷�İ뾶ΪR�����˶���P�����У��������߶�Ϊ��![]()
�����б���»��ľ���Ϊ��![]()
�ɻ�е���غ㶨���У� ![]()
�õ���![]() ��
��
��3����ϸ�ߵ�����ΪT������ţ�ٵڶ����ɿ��Եõ���
���M��![]()
��m��![]()
��ã�![]() (��
(��![]() ��
��![]() )��
)��

��ϰ��ϵ�д�
 �żӾ���ϵ�д�
�żӾ���ϵ�д�
�����Ŀ