��Ŀ����
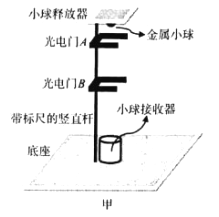
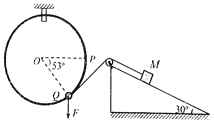
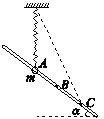
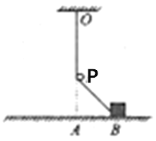
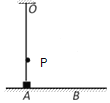
����Ŀ����ͼ��ʾ�����������̶����컨���ϵ�����O�ϣ��������������쳤ʱ����һ��λ��P�㣬��P��̶�һ���⻬��СԲ���������������¶�����һ���������λ�ڴֲڵ�ˮƽ�����ϵ�A���Ҷ�������ѹ����A��λ��P�����·����ְ���������ˮƽ�����ϵ�B�㾲ֹ�ͷţ�ˮƽ���������ڳ̶���ͬ�������������α�ʼ���ڵ������ڣ��ҷ��Ϻ��˶��ɡ�������B����A���˶��Ĺ����У�����˵����ȷ����
A. ����������֧����������
B. ����������Ħ�������ֲ���
C. ����ļ��ٶȽ�һֱ��С
D. �����뵯�������Ļ�е��֮����С
���𰸡�BD
��������
������B����A���˶��Ĺ����У���ֱ��������ƽ�⣬��ƽ�������ͺ��˶��ɷ����������ܵ�֧�����ı仯������Ӷ�����������Ħ�����仯�������ţ�ٵڶ����ɷ������ٶȵı仯��������ݹ��ܹ�ϵ����ϵͳ��е�ܵı仯�����
������B����A���˶��Ĺ����У��������˶���AB��ij��Cʱ��������ˮƽ����ļн�Ϊ![]() ���������쳤��Ϊx��������������
���������쳤��Ϊx��������������![]() ������������֧����Ϊ
������������֧����Ϊ![]() �����ֲ��䣬��
�����ֲ��䣬��![]() ��֪�����������Ļ���Ħ�������ֲ��䣬��A����B��ȷ��
��֪�����������Ļ���Ħ�������ֲ��䣬��A����B��ȷ��
����ţ�ٵڶ����ɵã�![]() ��x��С��
��x����![]() ����
����![]() ����
��С��![]() �ȴ���f�������f����С��f����֪���ٶ�a�ȼ�С��������C�����������B�˶���A�Ĺ����У����Ҫ�˷������Ħ�������������͵���������ɵ�ϵͳ��е����С����D��ȷ����ѡBD��
�ȴ���f�������f����С��f����֪���ٶ�a�ȼ�С��������C�����������B�˶���A�Ĺ����У����Ҫ�˷������Ħ�������������͵���������ɵ�ϵͳ��е����С����D��ȷ����ѡBD��

����Ŀ��ijͬѧ��ͼ����ʾ��·�����С���ݵķ����������ߣ��������£�
A��С���ݣ����ѹ2.5V�������0.25A��
B����������0��0.6A��
C����ѹ����0��3V��
D������������R1��0��10����
E������������R2��0��1000����
F���ɵ�أ��綯��Ϊ1.5V������
G�����أ���������
(1)����������Ӧѡ_____��ѡ������ǰ�Ĵ��ţ���
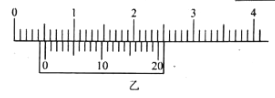
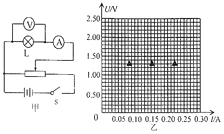
(2)ʵ���еõ����������±���ʾ�����ݱ�����������ͼ������С���ݵ�U��Iͼ��_________����ͼ���֪С���ݵĵ������¶ȵ����߶�_____��ѡ����������������С����������������
U/V | 0.20 | 0.40 | 0.60 | 1.00 | 1.40 | 1.80 | 2.00 | 2.20 |
I/A | 0.04 | 0.08 | 0.11 | 0.15 | 0.18 | 0.20 | 0.21 | 0.22 |
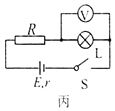
(3)ijͬѧ��һ�ڸɵ������ֵΪ5���ĵ���R��С���ݼ���ѹ�����ӳ�ͼ����ʾ��·���պ�S��ѹ����õ������˵�ѹΪ0.8V�����ͼ��ͼ��ͼ�����С����ʵ�����ĵĹ���Ϊ_____W���ɵ������Ϊ_____�����������������λ��Ч���֣�