题目内容
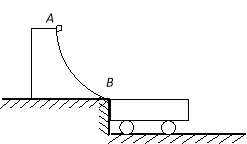
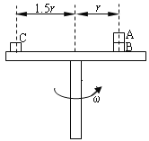
【题目】如图所示，有一内表面光滑的金属盒，底面长为L=1.5m，质量为m1=1kg，放在水平面上，与水平面间的动摩擦因数为μ=0.2，在盒内最右端放可看做质点的光滑金属球（半径忽略），质量为m2=1kg，现在盒的左端给盒施加一个水平冲量I=4Ns，（盒壁厚度，球与盒发生碰撞的时间和机械能损失均忽略不计）．g取10m/s2，求：
（1）金属盒能在地面上运动多远？
（2）金属盒从开始运动到最后静止所经历的时间多长？
【答案】（1）2m；（2）1.75s
【解析】（1）由于冲量作用，m1获得的速度为v=
=4m/s，（1分）
金属盒所受摩擦力为F=μ（m1+m2）g=4N，由于金属盒与金属球之间的碰撞没有能量损失，且金属盒和金属球的最终速度都为0，以金属盒和金属球为研究对象，由动能定理得：﹣Fs=0﹣
(2分）
解得：s=2m（1分）
（2）当盒前进s1=1.5m时与球发生碰撞，设碰前盒的速度为v1，碰后速度为v1′，球碰后速度为v2，则对盒，应用动能定理：
﹣Fs1=
﹣
，解得v1=2m/s（1分）
由于碰撞中动量守恒、机械能守恒，有：
m1v1=m1v1′+m2v2，
=
+
联立以上方程得：v1′=0，v2=2m/s．（1分）
当球前进1.5m时与盒发生第二次碰撞，碰撞前球的速度为2m/s，盒子的速度为0，碰撞后球的速度为0，盒子的速度变为v2=2m/s，
以金属盒为研究对象，利用动能定理得：
﹣Fs2=0﹣
，解得：s2=0.5m．（1分）
所以不会再与球碰，
则盒子运动时间可由动量定理给出：设盒子前进s1=1.5m所用时间为t1，前进s2=0.5m所用时间为t2，则：
﹣Ft1=m1v1﹣m1v，
﹣Ft2=0﹣m1v2，且v1=v2=2m/s
代入数据得：t1=0.5s，（1分）t2=0.5s（1分）
在盒两次运动之间还有一段时间t3为小球在运动，t3=s1/v2=0.75s
则金属盒从开始运动到最后静止所经历的时间t=t1+t2+t3=1.75s（1分）
