题目内容
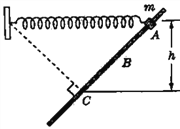
【题目】如图所示，水平转台上有一个质量为m的物块，用长为L的细绳将物块连接在转轴上，细线与竖直转轴的夹角为θ角，此时绳中张力为零，物块与转台间动摩擦因数为μ（μ＜tanθ），最大静摩擦力等于滑动摩擦力，物块随转台由静止开始缓慢加速转动，则下列说法正确的是（ ）
A. 转台一开始转动，细绳立即绷直对物块施加拉力
B. 当绳中出现拉力时，转台对物块做的功为μmgLsinθ
C. 当物体的角速度为
时，转台对物块支持力为零
D. 当转台对物块支持力为零时，转台对物块做的功为
【答案】D
【解析】转台一开始转动时，物体与转台之间的静摩擦力提供向心力，随转速的增加，静摩擦力逐渐变大，当达到最大静摩擦力时物块开始滑动，此时细绳绷直对物块施加拉力，选项A错误；
对物体受力分析知物块离开圆盘前
合力F=f+Tsinθ=m
①
N+Tcosθ=mg②
根据动能定理知W=Ek=
mv2③
当弹力T=0，r=Lsinθ④
由①②③④解得W=
fLsinθ≤
μmgLsinθ，至绳中出现拉力时，转台对物块做的功为
μmgLsinθ，故B错误；当N=0，f=0，由①②③知W=
mgLsinθtanθ=
，故D正确；由①②知
，所以当物块的角速度增大到
时，物块与转台间恰好无相互作用，故C错误；故选D.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
