Question

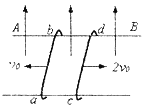
【题目】两固定水平平行金属导轨间距为L，导轨上放着两根相同导体棒和已知每根导体棒质量均为电阻均为R,导轨光滑且电阻不计,整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B，开始时和两导体棒有方向相反的水平初速度,大小分别为和求：

(1)从开始到最终稳定的过程中回路总共产生的焦耳热；

(2)当棒的速度大小变为时:

①通过棒的电量是多少?

②两棒间的距离增大了多少?

③回路消耗的电能为多少?

Answer 1

【答案】（1）mv02（2）①或②或△x2=③或

【解析】

（1）由于ab、cd两导体棒切割磁感线，回路中产生感应电流．它们在安培力得作用下做减速运动，由于两棒的质量相等，所受的安培力大小相等，cd棒的初速度较大，所以当ab减速为零时，cd棒仍在向右运动，以后cd棒继续减速，而ab棒反向加速，直到两棒达到共同速度后，回路中无感应电流，两棒以相同的速度v做匀速运动．对两棒组成的系统，合外力为零，系统的动量守恒，根据两棒总动量守恒和能量守恒求解从开始到最终稳定回路中产生的焦耳热．
（2）当ab棒的速度大小变为v0/4时有两种情况：一种速度方向向左，另一种速度方向向右．对两种情况，分别运用动量守恒定律求出cd棒的速度，再运用动量定理求通过cd棒的电荷量q，根据求两棒间的距离增加量．

（1）从开始到最终稳定的过程中，两棒的总动量守恒，取水平向右为正方向，由动量守恒定律有：2mv0-mv0=2mv共．
解得：v共=v0
由能量守恒定律可得从开始到最终稳定回路中总共产生的焦耳热为：
Q=mv02+m（2v0）2-（2m）v共2=mv02
（2）分析两种情况可知，当ab棒的速度大小是时有两种情况：
1°当ab棒的速度未反向，即向左时，设此时cd棒的速度是v1，根据动量守恒得：
2mv0-mv0=mv1-m
解得：v1=
2°当ab棒的速度反向即向右时，设此时cd棒的速度是v2，根据动量守恒得：
2mv0-mv0=mv1+m
解得：v2=
①对cd棒，由动量定理得 F安t=m△v
其中 F安=BIL，I=，E=BL（vcd-vab），q=It
代入两种情况可得，当vab=-时，有 BLq1=mv0-m
解得通过cd棒的电荷量为 q1=．
当vab′=时，有 BLq2=mv0+m
解得通过cd棒的电荷量为 q2=
②由
解得两棒间的距离增大△x1=或△x2=

③回路消耗的电能

或者