题目内容
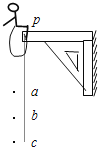
【题目】如图所示，长为L的轻绳竖直悬挂着一质量为m的小球A，恰好挨着放置在水平面上质量为m的物块B。现保持细绳绷直，把小球向左上方拉至细绳与竖直方向成60°角的位置，然后从静止释放小球。小球A到达最低点时恰好与物块B发生弹性碰撞，物块向右滑行了L的距离停下。求：
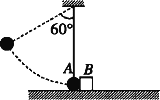
（1）物块与水平面间的动摩擦因数μ。
（2）若仅改变A的质量，使物块B与A发生弹性碰撞后能向右滑行的距离为2L，则小球A的质量应该多大。
【答案】（1）0.5 （2）
【解析】
（1）小球向下摆动过程机械能都守恒，根据机械能守恒分别求出碰撞前小球的速度大小．根据动量守恒定律以及能量守恒关系求出碰撞后物块的速度大小，根据动能定理研究向右滑动过程，求出物块与水平面间的动摩擦因数μ．
（2）小球向下摆动过程机械能都守恒．根据动量守恒定律以及能量守恒关系列出碰撞后物块和小球的速度关系式，根据动能定理研究向右滑动过程，联立方程求解小球A的质量．
（1）设小球与物块碰撞前瞬间的速度为v0，由机械能守恒定律得：
解得：
设碰撞后瞬间小球、物块的速度大小分别为v1、v2，由于碰撞是弹性的有：mv0＝mv1+mv2，
解得：
对于物块向右滑行的过程，由动能定理有：
μ＝0.5
（2）设小球与物块碰撞前瞬间的速度为v′0，由机械能守恒定律得：
解得：
设碰撞后瞬间有：Mv′0＝Mv′1+mv′2
解得：
若B物体前进2L停下则有：
得
则有
得：
练习册系列答案
名校课堂系列答案
相关题目
