题目内容
一蹦极运动员身系弹性蹦极绳从水面上方的高台下落，到最低点时距水面还有数米距离。假定空气阻力可忽略，运动员可视为质点，下列说法正确的是（ ）
| A．下落过程中运动员到达最低点前速度一直增大 |
| B．下落过程中，运动员的加速度先增大后减小。 |
| C．蹦极绳张紧后的下落过程中，蹦极绳的弹力对人做负功，弹性势能增加 |
| D．蹦极过程中，运动员、地球所组成的系统机械能守恒 |
C
解析试题分析：运动员先加速下落，再减速下落，直至最低点，A错误；下落过程中弹力逐渐增大，开始时重力大于弹力，后来弹力大于重力，合力（或加速度）先减小后增大，B错误；下落过程中，蹦极绳的弹力始终对人做负功，弹性势能增加，C正确；蹦极过程中，运动员、弹性绳、地球所组成的系统机械能守恒，D错误。
考点：本题考查了机械能守恒定律。
。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍，不考虑空气阻力、墙壁的摩擦阻力和物块落入圆弧轨道时的能量损失．求：
如图所示，重10 N的滑块在倾角为30°的斜面上，从a点由静止下滑，到b点接触到一个轻弹簧．滑块压缩弹簧到c点开始弹回，返回b点离开弹簧，最后又回到a点，已知ab＝0.8 m，bc＝0.4 m，那么在整个过程中( )
| A．弹簧弹性势能的最大值是6 J |
| B．滑块动能的最大值是6 J |
| C．从c到b弹簧的弹力对滑块做的功是6 J |
| D．滑块和弹簧组成的系统整个过程机械能守恒 |
两个质量不同的小铁块A和B，分别从高度相同且都光滑的斜面和圆弧斜面的顶点滑向底部，如图所示，如果它们的初速度都为零，则下列说法正确的是
| A．下滑过程中重力所做的功相等 | B．它们到达底部时动能相等 |
| C．它们到达底部时速率相等 | D．它们到达底部时速率不相等 |
在光滑的水平面上有三个完全相同的小球，它们成一条直线，2、3小球静止，并靠在一起，1小球以速度v0射向它们，如图所示．设碰撞中不损失机械能，则碰后三个小球的速度可能值是 
A．v1＝v2＝v3＝ v0 | B．v1＝0，v2＝v3＝ v0 |
C．v1＝0，v2＝v3＝ v0 | D．v1＝v2＝0，v3＝v0 |
如图所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球接触弹簧并将弹簧压缩至最低点（形变在弹性限度内），然后又被弹起离开弹簧，上升到一定高度后又下落，如此反复。通过安装在弹簧下端的压力传感器，测出该过程中弹簧弹力F随时间t变化的图象如图所示，则（ ）
| A．运动过程中小球的机械能守恒 |
| B．t2时刻小球的速度为零 |
| C．t1～t2这段时间内，小球的动能在逐渐减小 |
| D．t2～t3这段时间内，小球的动能与重力势能之和在减少 |
内壁光滑的环形凹槽半径为R，固定在竖直平面内，一根长度为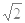
R的轻杆，一端固定有质量m的小球甲，另一端固定有质量为2m的小球乙．现将两小球放入凹槽内，小球乙位于凹槽的最低点（如图所示），由静止释放后 
| A．下滑过程中甲球的机械能变化量大小总是等于乙球的机械能变化量大小 |
| B．下滑过程中甲球减少的重力势能总是等于乙球增加的重力势能 |
| C．甲球可沿凹槽下滑到槽的最低点 |
| D．杆从右向左滑回时，乙球一定能回到凹槽的最低点 |
如图所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的环，环套在竖直固定的光滑直杆上，光滑的轻小定滑轮与直杆的距离为d，杆上的A点与定滑轮等高，杆上的B点在A点下方距离A为d处。现将环从A处由静止释放，不计一切摩擦阻力，下列说法正确的是
A．环到达B处时，重物上升的高度 |
B．环到达B处时，环与重物的速度大小之比为 |
| C．环从A到B，环减少的机械能大于重物增加的机械能 |
D．环能下降的最大高度为 |
如图所示，从光滑的1/ 4圆弧槽的最高点滑下的小滑块，滑出槽口时速度方向为水平方向，槽口与一个半球顶点相切，半球底面为水平，若要使小物块滑出槽口后不沿半球面下滑，已知圆弧轨道的半径为R1，半球的半径为R2，则R1和R2应满足的关系是
| A．R1≤R2/2 |
| B．R1≥R2/2 |
| C．R1≤R2 |
| D．R1≥R2 |