题目内容
 某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.20cm;用20分度的游标卡尺测小球直径如图所示,然后用秒表记录了单摆全振动50次所用的时间为100.0s.则
某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.20cm;用20分度的游标卡尺测小球直径如图所示,然后用秒表记录了单摆全振动50次所用的时间为100.0s.则(1)记录时间应从摆球经过
平衡位置
平衡位置
开始计时,小球直径为2.990
2.990
cm,测得重力加速度g值为9.73
9.73
m/s2.(保留小数点后两位有效数字)(2)如果他在实验中误将49次全振动数为50次,测得的g值
偏大
偏大
.(填“偏大”或“偏小”或“准确”)(3)如果该同学在测摆长时忘记了加摆球的半径,则测量结果
偏小
偏小
(填“偏大”或“偏小”或“准确”);但是他以摆长(l)为纵坐标、周期的二次方(T2)为横坐标作出了l-T2图线,由图象测得的图线的斜率为k,则测得的重力加速度g=4π2k
4π2k
.(用字母表示即可).此时他用图线法求得的重力加速度准确
准确
.(选填“偏大”,“偏小”或“准确”)分析:单摆在摆角比较小时,单摆的运动才可以看成简谐运动.摆球经过平衡位置时速度最大,此时计时,误差比较小.根据单摆的公式T=2π
,推导出g的表达式.再根据g的表达式分析误差形成的原因.
|
解答:解:(1)单摆摆球经过平衡位置的速度最大,最大位移处速度为0,在平衡位置计时误差最小;
由图可知,小球的直径D=29mm+0.05mm×18=29.90mm=2.990cm;
单摆的摆长为L+
,单摆的周期T=
,根据单摆的公式T=2π
,所以g=
=
m/s2=9.73m/s2.
(2)试验中将49次全振动数为50次,会导致测得周期偏小,根据g=
,知测得重力加速度偏大.
(3)如果测摆长时忘记了加摆球的半径,会导致测得摆长偏小,根据g=
,知测得重力加速度偏小.
图线的斜率为k=
,由公式g=
可知,g=4π2k.
作l-T2图象,求重力加速度误差最小,因为描点后画线时要求尽可能多的点在该直线上,其余点尽可能均衡地分布在该直线两侧;
故答案为:(1)平衡位置,2.990,9.73;
(2)偏大;
(3)偏小,4π2k,准确.
由图可知,小球的直径D=29mm+0.05mm×18=29.90mm=2.990cm;
单摆的摆长为L+
| D |
| 2 |
| t |
| n |
|
4π2(L+
| ||
| t2 |
4×3.142×(97.20+
| ||
| 1002 |
(2)试验中将49次全振动数为50次,会导致测得周期偏小,根据g=
| 4π2L |
| T2 |
(3)如果测摆长时忘记了加摆球的半径,会导致测得摆长偏小,根据g=
| 4π2L |
| T2 |
图线的斜率为k=
| L |
| T2 |
| 4π2L |
| T2 |
作l-T2图象,求重力加速度误差最小,因为描点后画线时要求尽可能多的点在该直线上,其余点尽可能均衡地分布在该直线两侧;
故答案为:(1)平衡位置,2.990,9.73;
(2)偏大;
(3)偏小,4π2k,准确.
点评:解决本题的关键掌握单摆的周期公式T=2π
,以及知道测量时形成误差的原因.
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
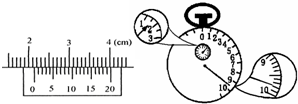 ①某同学在做“利用单摆测重力加速度“实验中先测得摆线长为97.44cm,球直径由如图游标卡尺测得.然后用秒表记录了单摆振动50次所用的时间如图所示,则:小球直径为
①某同学在做“利用单摆测重力加速度“实验中先测得摆线长为97.44cm,球直径由如图游标卡尺测得.然后用秒表记录了单摆振动50次所用的时间如图所示,则:小球直径为

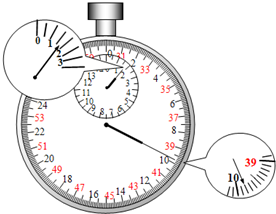 某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.5厘米,摆球直径2.0厘米,然后用秒表记录了单摆振动50次所用的时间如图.
某同学在做“利用单摆测重力加速度”实验中,先测得摆线长为97.5厘米,摆球直径2.0厘米,然后用秒表记录了单摆振动50次所用的时间如图.