题目内容
4.质量为2t的汽车发动机额定功率为80kW,若汽车在平直公路上行驶所受阻力大小恒为4×103N.求:(1)汽车在公路上的最大行驶速度的大小;
(2)汽车以额定功率起功,当汽车速度为5m/s时的加速度的大小;
(3)汽车以2m/s2的加速度起动做匀加速运动所能维持的时间.
分析 (1)当汽车的牵引力与阻力相等时,速度最大,结合牵引力和额定功率求出汽车行驶的最大速度.
(2)根据功率与速度的关系求出牵引力,再根据牛顿第二定律求解加速度.
(3)根据牛顿第二定律求出汽车牵引力的大小,根据功率求出匀加速直线运动的最大速度,结合速度时间公式求出汽车匀加速直线运动的时间.
解答 解:(1)当牵引力等于阻力时,汽车的加速度a=0,行驶的速度最大
${v}_{m}^{\;}=\frac{P}{F}=\frac{P}{f}=\frac{80×1{0}_{\;}^{3}}{4×1{0}_{\;}^{3}}m/s=20m/s$
(2)当速度v=5m/s时牵引力$F=\frac{P}{v}=\frac{80×1{0}_{\;}^{3}}{5}=16×1{0}_{\;}^{3}N$
根据牛顿第二定律,有F-f=ma
得$a=\frac{F-f}{m}=\frac{16×1{0}_{\;}^{3}-4×1{0}_{\;}^{3}}{2×1{0}_{\;}^{3}}m/{s}_{\;}^{2}=6m/{s}_{\;}^{2}$
(3)根据牛顿第二定律F-f=ma
得$F=f+ma=4×1{0}_{\;}^{3}+2×1{0}_{\;}^{3}×2$=$8×1{0}_{\;}^{3}$N
匀加速直线运动的最大速度${v}_{1}^{\;}=\frac{P}{F}=\frac{80×1{0}_{\;}^{3}}{8×1{0}_{\;}^{3}}m/s=10m/s$
匀加速运动的时间${t}_{1}^{\;}=\frac{{v}_{1}^{\;}}{a}=\frac{10}{2}s=5s$
答:(1)汽车在公路上的最大行驶速度的大小为20m/s;
(2)汽车以额定功率起功,当汽车速度为5m/s时的加速度的大小6$m/{s}_{\;}^{2}$;
(3)汽车以2m/s2的加速度起动做匀加速运动所能维持的时间为5s
点评 解决本题的关键会通过汽车受力情况判断其运动情况,知道汽车在平直路面上行驶时,当牵引力与阻力相等时,速度最大.

 天天向上口算本系列答案
天天向上口算本系列答案| A. | 只要物体质量很小,就可以看成质点 | |
| B. | 只要物体体积很小,就可以看成质点 | |
| C. | 只要物体是球体,就可以看成质点 | |
| D. | 质点既具有数学特征,又具有物理属性 |
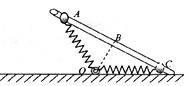 如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )
如图所示,轻质弹簧一端固定在水平面上O点的转轴上,另一端与一质量为m、套在粗糙固定直杆A处的小球(可视为质点)相连,直杆的倾角为30°,OA=OC,B为AC的中点,OB等于弹簧原长.小球从A处由静止开始下滑,初始加速度大小为aA,第一次经过B处的速度为v,运动到C处速度为0,后又以大小为aC的初始加速度由静止开始向上滑行.设最大静摩擦力等于滑动摩擦力.下列说法不正确的是( )| A. | 小球可以返回到出发点A处 | |
| B. | 弹簧具有的最大弹性势能为$\frac{1}{2}$mv2 | |
| C. | 撤去弹簧,小球可以在直杆上处于静止 | |
| D. | aA-aC=g |
| A. | 凡轻小的物体皆可看作质点,而体积较大的物体不能看作质点 | |
| B. | 作息时间表上的数字表示时间间隔 | |
| C. | 物体做单向直线运动时,其位移就是路程 | |
| D. | 跳水运动员起跳后,到达最高点的速度为瞬时速度 |
| A. | a越大,V也越大 | B. | a越大,△V也越大 | ||
| C. | a为正,V为负是不可能的 | D. | a为正,△V为负是不可能的 |
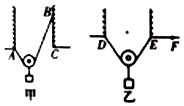 有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )
有甲、乙两根完全相同的轻绳,甲绳A、B两端按图甲的方式固定,然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上,当滑轮静止后,设绳子的张力大小为T1;乙绳两端按图乙的方式连接,然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上,当滑轮静止后,设乙绳子的张力大小为T2.现甲绳的B端缓慢向下移动至C点,乙绳的E端缓慢移动至F点,在两绳的移动过程中,下列说法正确的是( )| A. | T1、T2都变大 | B. | T1变大、T2变小 | C. | T1、T2都不变 | D. | T1不变、T2变大 |
| A. | 500W | B. | 25W | C. | 2000W | D. | 475W |
 如图所示,传送带与地面的倾角θ=37o,从A到B的长度为16m,传送带以V0=10m/s的速度逆时针转动.在传送带上端无初速的放一个质量为0.5㎏的物体,它与传送带之间的动摩擦因数μ=0.5,(sin37°=0.6,cos37°=0.8)求:
如图所示,传送带与地面的倾角θ=37o,从A到B的长度为16m,传送带以V0=10m/s的速度逆时针转动.在传送带上端无初速的放一个质量为0.5㎏的物体,它与传送带之间的动摩擦因数μ=0.5,(sin37°=0.6,cos37°=0.8)求: 如图所示,质量为50kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑100m到达坡底,用时10s.若g取10m/s2,求:
如图所示,质量为50kg的滑雪运动员,在倾角θ为30°的斜坡顶端,从静止开始匀加速下滑100m到达坡底,用时10s.若g取10m/s2,求: