题目内容
【题目】如图所示，光滑水平面上有一质量M=4．0kg的平板车，车的上表面右侧是一段长L=1．0m的水平轨道，水平轨道左侧是一半径R=0．25m的1/4光滑圆弧轨道，圆弧轨道与水平轨道在O′点相切．车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m=1．0kg的小物块（可视为质点）紧靠弹簧，小物块与水平轨道间的动摩擦因数μ=0．5．整个装置处于静止状态．现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A．不考虑小物块与轻弹簧碰撞时的能量损失，不计空气阻力，取g=10m/s2．求：
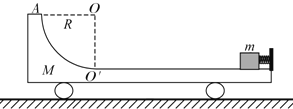
（1）解除锁定前弹簧的弹性势能；
（2）小物块第二次经过O′点时的速度大小；
（3）小物块与车最终相对静止时距O′点的距离
【答案】（1）7．5J（2）2．0m/s（3）0．5m
【解析】
试题分析：（1）平板车和小物块组成的系统，水平方向动量守恒，解除锁定前，总动量为零，故小物块到达圆弧最高点A时，二者的共同速度v共=0
设弹簧解除锁定前的弹性势能为Ep，上述过程中系统能量守恒，则有
Ep=mgR+μmgL
代入数据解得 Ep=7．5J
（2）设小物块第二次经过O'时的速度大小为vm，此时平板车的速度大小为vM，研究小物块在平板车圆弧面上的下滑过程，由系统动量守恒和机械能守恒有0=mvm-MvM
mgR＝
mvm2+MvM2
代入数据解得 vm=2．0m/s
（3）最终平板车和小物块相对静止时，二者的共同速度为0．
设小物块相对平板车滑动的路程为S，对系统由能量守恒有
Ep=μmgS
代入数据解得S=1．5m
则距O'点的距离x=S-L=0．5m
阅读快车系列答案
【题目】利用如图(a)所示电路可以测量金属丝的电阻率ρ，所用的实验器材有：
待测的粗细均匀的电阻丝、电流表(量程0.6 A，内阻忽略不计)
电源(电动势3.0 V，内阻r未知)、保护电阻(R0＝4.0 Ω)
刻度尺、开关S、导线若干、滑片P
实验步骤如下：
①用螺旋测微器测得电阻丝的直径d如图(b)所示。
②闭合开关，调节滑片P的位置，分别记录每次实验中aP长度x及对应的电流值I。
③以
为纵坐标，x为横坐标，作
x图线(用直线拟合)。
④求出直线的斜率k和在纵轴上的截距b。
回答下列问题：
(1)螺旋测微器示数为d ＝________mm。
(2)用题中字母可求得
与x满足的关系式为________。
(3)实验得到的部分数据如下表所示，其中aP长度x＝0.30 m时电流表的示数如图(a)所示，读出数据，完成下表。①________；②________。
x(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
I(A) | 0.49 | 0.43 | ① | 0.33 | 0.31 | 0.28 |
| 2.04 | 2.33 | ② | 3.03 | 3.23 | 3.57 |
(4)在图(b)的坐标纸上将所缺数据点补充完整并作图，根据图线求得斜率k＝______－1·m－1，截距b＝________A－1。(保留两位小数)
(5)根据图线求得电阻丝的电阻率ρ ＝_______Ω·m，电源的内阻为r ＝________Ω。(保留一位小数)
