题目内容
【题目】如图，两劲度系数均为k的同样的轻弹性绳的上端固定在一水平面上，下端悬挂一质量为m的小物块。平衡时，轻弹性绳与水平面的夹角为
0，弹性绳长度为l0．现将小物块向下拉一段微小的距离后从静止释放。
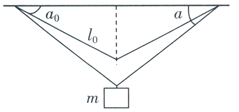
（1）证明小物块做简谐振动；
（2）若k=0.50N/m、m=50g、0=30°、l0=2.0m，重力加速度g=9.8 m/s。，求小物块做简谐振动的周期T；
（3）当小物块下拉的距离为0.010m时，写出此后该小物块相对于平衡位置的偏离随时间变化的方程。已知：当x<<1时，
，
．
【答案】（1）F回=－(2ksin2α0+
)y；（2）1.8s；（3）y=0.010×cos(3.5×t)
【解析】
（1）取小物块的平衡位置为原点O，y轴的方向竖直向下，如图所示：
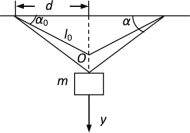
由牛顿第二定律可知
ma=mg－2k(l－L)sinα ①
式中a为物块的加速度，L为弹性绳的原长；l0为物块静止时，弹性绳的长；l和
分别为物块离开平衡位置的位移为y时弹性绳的长度和弹性绳与水平面的夹角。
由几何关系得
l=
②
sinα=
③
d=l0cosα0 ④
④代入② 展开，化简得
l=
由于y是小量，y2是二阶无穷小量，可略去。得
l=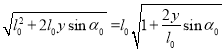
由小量展开式：当x<<1时，
，知
l=
=l0+ysinα0 ⑤
将⑤代入③，得
sinα=
由 当x<<1时，
，知
sinα=(l0sinα0+y)[
(1－
sinα0)]
l0sinα= l0sinα0+y－y sin2α0－(y2/l0)sinα0
且 忽略y2项
l0sinα= l0sinα0+ycos2α0
sinα= sinα0+(y/l0)cos2α0 ⑥
当小物块处在平衡位置时有
mg=2k(l0－L)sinα0
即
L =l0－
⑦
⑤⑥⑦(代去l，L，sinα)代入① 得
ma=mg－2k[l0+ysinα0－l0+][ sinα0+(y/l0)cos2α0 ]
ma=mg－2k[ysin2α0+ 
+ 
]
略去y2项
ma=－(2ksin2α0+)y
由简谐运动的特征方程知
F回=－Ky
所以
K=(2ksin2α0+)
即
F回=－(2ksin2α0+)y
由此，物体的运动满足简谐运动的特征方程。因此，当y很小时，小物块做简谐运动。
（2）小物块做简谐运动的周期为
T=2π
= 
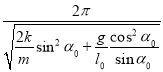⑧
将题给数据代入⑧，得小物块做简谐振动的周期
T=1.8s
（3）因将小物块拉开距离y0=0.010m 时从静止松手，故小物块做简谐振动的振幅为A=0.010m，初始时，小物块速度为零，小物块位于最大振幅处，其初相位为
φ0=0 ⑨
圆频率为
ω0=
故在国际单位制中，小物块做简谐振动的方程为
y=0.010cos(3.5t)
