题目内容
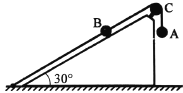
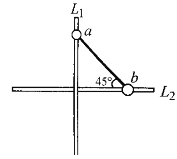
【题目】如图所示,竖直平面内固定两根足够长的细杆L1、L2,两杆分离不接触,且两杆间的距离忽略不计。两个小球a、b(视为质点)质量均为m,a球套在竖直杆L1上,b杆套在水平杆L2上,a、b通过铰链用长度为![]() 的刚性轻杆连接,将a球从图示位置由静止释放(轻杆与L2杆夹角为45°),不计一切摩擦,已知重力加速度为g。在此后的运动过程中,下列说法中正确的是
的刚性轻杆连接,将a球从图示位置由静止释放(轻杆与L2杆夹角为45°),不计一切摩擦,已知重力加速度为g。在此后的运动过程中,下列说法中正确的是
A. a球和b球所组成的系统机械能守恒
B. b球的速度为零时,a球的加速度大小一定等于g
C. b球的最大速度为![]()
D. a球的最大速度为![]()
【答案】ABC
【解析】
a球和b球组成的系统没有外力做功,只有a球和b球的动能和重力势能相互转换,因此a球和b球的机械能守恒,A正确;
设轻杆L和水平杆L2的夹角为![]() ,由运动关联可知
,由运动关联可知![]() ,得
,得![]() 可知当b球的速度为零时,轻杆L处于水平位置和L2杆平行,因此此时a球在竖直方向只受重力
可知当b球的速度为零时,轻杆L处于水平位置和L2杆平行,因此此时a球在竖直方向只受重力![]() ,因此a球的加速度大小为
,因此a球的加速度大小为![]() ,B正确;
,B正确;
当杆L和杆L1平行成竖直状态,球a运动到最下方,球b运动到L1和L2交点的位置的时候球b的速度达到最大,此时由运动的关联可知a球的速度为0,因此由系统机械能守恒有![]() ,得
,得![]() 。C正确;
。C正确;
当轻杆L向下运动到杆L1和杆L2的交点的位置时,此时杆L和杆L2平行,由运动的关联可知此时b球的速度为零,有系统机械能守恒有![]() ,得
,得![]() 此时a球具有向下的加速度
此时a球具有向下的加速度![]() ,因此此时a球的速度不是最大,a球将继续向下运动到加速度为0时速度达到最大,D错误。
,因此此时a球的速度不是最大,a球将继续向下运动到加速度为0时速度达到最大,D错误。

练习册系列答案
相关题目