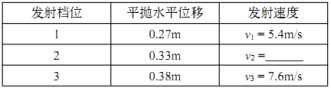
题目内容
【题目】一个质量m = 0.1g的小滑块,带有q=5×10-4C的电荷,放置在倾角α=450 的光滑斜面上(斜面绝缘),斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面下滑,其斜面足够长,小滑块滑至某一位置时,要离开斜面。问:

(1)小滑块带何种电荷?
(2)小滑块离开斜面时的瞬时速度多大?
(3)该斜面的长度至少多长?
【答案】(1)负电(2)2![]() m/s(3)
m/s(3)![]()
【解析】
(1)带电滑块在滑至某一位置时,由于在洛伦兹力的作用下,要离开斜面。根据磁场方向结合左手定则可得带电粒子的电性。
(2)由光滑斜面,所以小滑块在没有离开斜面之前一直做匀加速直线运动。借助于洛伦兹力公式可求出恰好离开时的速度大小,
(3)根据动能定理求出位移大小。
(1)小滑块沿斜面下滑过程中,受重力mg、斜面支持力N和洛伦兹力F.若要小滑块离开斜面,洛伦兹力F方向应垂直斜面向上,根据左手定则可知,小滑块应带负电荷。
(2)小滑块沿斜面下滑时,垂直斜面方向的加速度为零,有:
qvB+N-mgcosα=0
当N=0时,小滑块开始脱离斜面,此时有:qvB=mgcosα
得:![]()
(3)下滑过程中,只有重力做功,由动能定理得:
mgxsinα=![]() mv2
mv2
斜面的长度至少应是:![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目