Question

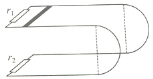
【题目】如图所示，有上下放置的两个宽度均为L=0.5m的水平金属导轨，左端连接阻值均为2的电阻r1、r2，右端与竖直放置的两个相同的半圆形金属轨道连接在一起，半圆形轨道半径为R=0.1 m。整个装置处在竖直向上的匀强磁场中，磁感应强度为B=2T。初始时金属棒放置在上面的水平导轨上，金属棒的长刚好为L，质量m=2kg，电阻不计。某时刻金属棒获得了水平向右的速度v0=2m/s，之后恰好水平抛出。已知金属棒与导轨接触良好，重力加速度g=10m/s2，不计所有摩擦和导轨的电阻，则下列正确的是

A. 金属棒抛出时的速率为

B. 整个过程中，流过电阻r1的电荷量为2C

C. 整个过程中，电阻r2上产生的焦耳热为1.5J

D. 最初金属棒距离水平导轨右端4m

Answer 1

【答案】C

【解析】

金属棒经过半圆形金属轨道的时候恰好水平抛出说明在此点只有重力提供向心力，因此有，。A错误；

取向右为正，对导体棒写动量定理有代入数据解得，因导体棒在运动的时候相当于电源，电阻r1和电阻r2串联，故流过电阻r1的电荷量为导体棒电荷量的一半，即1C，所以B错误；

由能量转换可知，导体棒损失的动能转化为电阻r1和电阻r2消耗的焦耳热，而电阻r1和电阻r2并联且任何时候电流都一样，因此焦耳热也一样，因此有，，C对；

由，得，则最初导体棒离右端的距离为8m，D错误。