题目内容
【题目】如图所示，内壁光滑的圆形轨道半径为R，固定在竖直平面内，圆形轨道上的P、Q两点与圆心O等高，N为轨道的最高点;质量均为m的小球(可视为质点)A和B，以等大的速率v0同时从P处向上、向下滑入圆形轨道，若在运动过程中两球均未脱离圆形轨道，重力加速度为g。下列说法正确的是
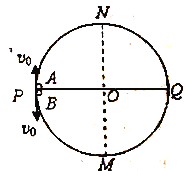
A. 两球第一次相遇点一定在N、Q之间
B. 两球第一次相遇点可能在P、N之间
C. 两球从P点释放到第一次相遇，重力的冲量相同
D. 小球A通过最高点时的机械能小于小球B通过最低点时的机械能
【答案】AC
【解析】试题分析：两个小球在光滑的圆轨道内运动，机械能守恒，据机械能守恒定律分析它们再次相遇时速率关系以及位置关系，机械能关系．
A向上先做减速运动，越过最高点后再做加速运动，B向下先做加速运动，越过最低点后再做减速运动，到达Q点时，两者速率相等，则从P运动到Q点的过程中A球的平均速率小于B球的平均速率，所以两球再次相遇时应在Q点的上方，即在NQ之间，A正确B错误；因为相遇时运动的时间相同， 
，质量也相同，所以重力的重力相同，C正确；两球开始出发时机械能相等，运动过程中各自的机械能守恒，则小球A通过最高点时的机械能等于小球B通过最低点时的机械能，D错误．
练习册系列答案
相关题目
