题目内容
7. 如图,在x轴上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;在x轴下方存在匀强电场,场强大小为E,电场方向与xoy平面平行,且与x轴成450夹角.一质量为m、电荷量为q(q>0)的粒子以速度v0从y轴上P点沿y轴正方向射出,一段时间后进入电场,进入电场时的速度方向与电场方向相反;从粒子进入电场开始经过某一段时间T0(T0未知),磁场方向变为垂直纸面向里,大小不变,结果能使粒子返回到P点(不计粒子重力)
如图,在x轴上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外;在x轴下方存在匀强电场,场强大小为E,电场方向与xoy平面平行,且与x轴成450夹角.一质量为m、电荷量为q(q>0)的粒子以速度v0从y轴上P点沿y轴正方向射出,一段时间后进入电场,进入电场时的速度方向与电场方向相反;从粒子进入电场开始经过某一段时间T0(T0未知),磁场方向变为垂直纸面向里,大小不变,结果能使粒子返回到P点(不计粒子重力)(1)粒子磁场中运动半径R
(2)粒子第一次经过x轴时的坐标位置
(3)从P点出发到再次回到P点的时间.
分析 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径;
(2)根据粒子轨道半径,应用几何知识可以求出x轴的坐标;
(3)求出粒子在电场与磁场中的运动时间,然后求出总的运动时间.
解答 解:(1)粒子做匀速圆周运动,洛伦兹力提供向心力,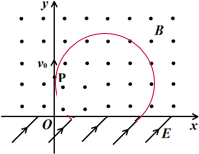
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{R}$,解得:R=$\frac{m{v}_{0}}{qB}$;
(2)粒子运动轨迹如图所示,
由几何知识得:x=R+Rcos45°=$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$;
(3)粒子在磁场中转过的圆心角:θ=180°+45°=225°,
粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中运动的时间:t1=2×$\frac{θ}{360°}$T=$\frac{5πm}{2qB}$,
粒子在电场中的运动时间:t2=2×$\frac{{v}_{0}}{a}$=2×$\frac{{v}_{0}}{\frac{qE}{m}}$=$\frac{2m{v}_{0}}{qE}$,
粒子回到P点的时间:t=t1+t2=$\frac{5πm}{2qB}$+$\frac{2m{v}_{0}}{qE}$;
答:(1)粒子磁场中运动半径R为$\frac{m{v}_{0}}{qB}$;
(2)粒子第一次经过x轴时的坐标位置为$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$;
(3)从P点出发到再次回到P点的时间为$\frac{5πm}{2qB}$+$\frac{2m{v}_{0}}{qE}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程、确定粒子运动性质是正确解题的关键,应用牛顿第二定律与粒子做圆周运动的周期公式即可解题.

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | 高大建筑安装避雷针 | B. | 油罐车后面装一条拖地的铁链 | ||
| C. | 静电复印 | D. | 印刷车间内保持适当的湿度 |

| A. | 甲图象可求电源的电动势和内电阻 | B. | 乙图象可求电源的电动势和内电阻 | ||
| C. | 丙图象可求滑动变阻器的阻值 | D. | 丙图象可求电阻R0的阻值 |
 一个实验小组的同学设计了一个测量动摩擦因数的实验,如图甲所示,把弹簧测力计的一端固定在墙上,另一端与一物块A相连,用力F水平向左拉物块下面的金属板B,金属板B向左运动,此时测力计的示数稳定(图乙中已把测力计的示数放大画出),则物块A与金属板B间的滑动摩擦力的大小是2.6N,若用弹簧测力计测得物块A重13.00N,根据下面表格中给出的动摩擦因数,则可推算出物块A的材料是木头---金属
一个实验小组的同学设计了一个测量动摩擦因数的实验,如图甲所示,把弹簧测力计的一端固定在墙上,另一端与一物块A相连,用力F水平向左拉物块下面的金属板B,金属板B向左运动,此时测力计的示数稳定(图乙中已把测力计的示数放大画出),则物块A与金属板B间的滑动摩擦力的大小是2.6N,若用弹簧测力计测得物块A重13.00N,根据下面表格中给出的动摩擦因数,则可推算出物块A的材料是木头---金属| 材料 | 动摩擦因数 |
| 金属--金属 | 0.25 |
| 橡胶--金属 | 0.30 |
| 木头--金属 | 0.20 |
| 皮革--金属 | 0.28 |
| A. | 0.8m | B. | 1.0m | C. | 1.6m | D. | 2.0m |
 如图所示,一个很长的竖直放置的圆柱形磁铁,在其外部产生一个中心辐射磁场(磁场水平向外),其大小为B=$\frac{k}{r}$(其中r为辐射半径--考察点到圆柱形磁铁中心轴线的距离,k为常数),设一个与磁铁同轴的圆形铝环,半径为R(大于圆柱形磁铁的半径),制成铝环的铝丝其横截面积为S,铝环由静止下落通过磁场,下落过程中铝环平面始终水平,已知铝丝电阻率为ρ,密度为ρ0,当地重力加速度为g,试求:
如图所示,一个很长的竖直放置的圆柱形磁铁,在其外部产生一个中心辐射磁场(磁场水平向外),其大小为B=$\frac{k}{r}$(其中r为辐射半径--考察点到圆柱形磁铁中心轴线的距离,k为常数),设一个与磁铁同轴的圆形铝环,半径为R(大于圆柱形磁铁的半径),制成铝环的铝丝其横截面积为S,铝环由静止下落通过磁场,下落过程中铝环平面始终水平,已知铝丝电阻率为ρ,密度为ρ0,当地重力加速度为g,试求:
 如图所示的电路中,电炉电阻R=10Ω,电动机线圈的电阻r=1Ω,电路两端电压U=100V,电流表的示数30A,问通过电动机的电流为多少?通电一分钟,电动机做的有用功为多少?
如图所示的电路中,电炉电阻R=10Ω,电动机线圈的电阻r=1Ω,电路两端电压U=100V,电流表的示数30A,问通过电动机的电流为多少?通电一分钟,电动机做的有用功为多少?