题目内容
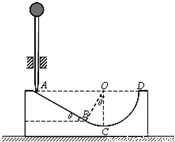
质量为m的小球固定在光滑轻细杆的上端,细杆通过光滑的限位孔且保持竖直.在光滑水平面上放置一个质量为M=2m的凹形槽,凹形槽的光滑内表面如图所示,AB部分是斜面,与水平面成θ=30°,BCD部分是半径为R的圆弧面,AB与BCD两面在B处相切.让细杆的下端与凹形槽口的左边缘A点接触.现将小球释放,求:(1)当轻细杆的下端滑到凹形槽的最低点C时,凹形槽的速度是多大;
(2)轻细杆的下端能否运动到凹形槽口的右边缘 D点;(回答“能”或“不能”,并简述理由)
(3)当轻细杆的下端滑到B点的瞬间,小球和凹形槽的速度各是多大.
【答案】分析:(1)当轻细杆的下端运动到最低点C时,小球的速度为零.以小球和凹形槽组成的系统,机械能守恒,根据机械能守恒定律求出凹形槽的速度.
(2)判断系统有无能量损失,若满足机械能守恒,则可以到达D点;
(3)当轻细杆的下端滑到B点的瞬间,根据运动的合成与分解槽和球的速度关系,再由系统机械能守恒求出两个物体的速度.
解答: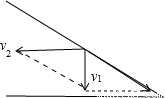 解:(1)当轻细杆的下端运动到最低点C时,小球的速度为零,小球减少的重力势能转化为凹形槽的动能,由能量转化守恒定律
解:(1)当轻细杆的下端运动到最低点C时,小球的速度为零,小球减少的重力势能转化为凹形槽的动能,由能量转化守恒定律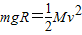
又因为:M=2m
得凹形槽的速度: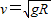
(2)能.原因:球、滑块组成的系统满足机械能守恒.
(3)当轻细杆的下端从A点相对滑动到B点时,
小球的速度v1与凹形槽的速度v2之间的关系如右图所示:得:v1=v2tanθ
由系统能量转化守恒定律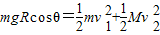
又 M=2m
解得: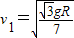
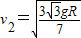
答:(1)当轻细杆的下端滑到凹形槽的最低点C时,凹形槽的速度是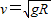 ;
;
(2)轻细杆的下端能运动到凹形槽口的右边缘 D点,因为系统机械能守恒;
(3)当轻细杆的下端滑到B点的瞬间,小球和凹形槽的速度分别是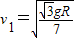 和
和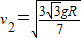
点评:本题难点在于分析小球的速度与凹形槽的速度的关系,关键理解物体的实际运动为合运动,根据合运动与分运动的矢量关系求解速度关系.
(2)判断系统有无能量损失,若满足机械能守恒,则可以到达D点;
(3)当轻细杆的下端滑到B点的瞬间,根据运动的合成与分解槽和球的速度关系,再由系统机械能守恒求出两个物体的速度.
解答:
 解:(1)当轻细杆的下端运动到最低点C时,小球的速度为零,小球减少的重力势能转化为凹形槽的动能,由能量转化守恒定律
解:(1)当轻细杆的下端运动到最低点C时,小球的速度为零,小球减少的重力势能转化为凹形槽的动能,由能量转化守恒定律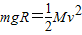
又因为:M=2m
得凹形槽的速度:
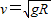
(2)能.原因:球、滑块组成的系统满足机械能守恒.
(3)当轻细杆的下端从A点相对滑动到B点时,
小球的速度v1与凹形槽的速度v2之间的关系如右图所示:得:v1=v2tanθ
由系统能量转化守恒定律
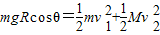
又 M=2m
解得:
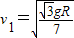
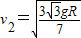
答:(1)当轻细杆的下端滑到凹形槽的最低点C时,凹形槽的速度是
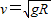 ;
;(2)轻细杆的下端能运动到凹形槽口的右边缘 D点,因为系统机械能守恒;
(3)当轻细杆的下端滑到B点的瞬间,小球和凹形槽的速度分别是
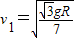 和
和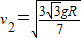
点评:本题难点在于分析小球的速度与凹形槽的速度的关系,关键理解物体的实际运动为合运动,根据合运动与分运动的矢量关系求解速度关系.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图所示,长为L、内壁光滑的直管与水平地面成30°角固定位置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=3m的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变(重力加速度为g).
如图所示,长为L、内壁光滑的直管与水平地面成30°角固定位置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=3m的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变(重力加速度为g). 如图所示,质量为m的小球固定在杆的一端,在竖直面内绕杆的另一端做圆周运动,当小球运动到最高点时,瞬时速度v=
如图所示,质量为m的小球固定在杆的一端,在竖直面内绕杆的另一端做圆周运动,当小球运动到最高点时,瞬时速度v= (2011?江苏)如图所示,长为L、内壁光滑的直管与水平地面成30°角固定放置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变.(重力加速度为g)
(2011?江苏)如图所示,长为L、内壁光滑的直管与水平地面成30°角固定放置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变.(重力加速度为g) 质量为m的小球固定在光滑轻细杆的上端,细杆通过光滑限位孔保持竖直.在光滑水平面上放置一质量为M=2m的凹形槽,凹形槽的光滑内表面如图所示,AB部分是斜面,与水平面成θ=30°,BCD部分是半径为R的圆弧面,AB与BCD两面在B处相切.让细杆的下端与凹形槽口的左边缘A点接触.现将小球释放,求:
质量为m的小球固定在光滑轻细杆的上端,细杆通过光滑限位孔保持竖直.在光滑水平面上放置一质量为M=2m的凹形槽,凹形槽的光滑内表面如图所示,AB部分是斜面,与水平面成θ=30°,BCD部分是半径为R的圆弧面,AB与BCD两面在B处相切.让细杆的下端与凹形槽口的左边缘A点接触.现将小球释放,求: 如图所示,质量为m的小球固定在长为L的细轻杆的一端,绕细杆的另一端O在竖直平面上做圆周运动.球转到最高点A时,线速度的大小为
如图所示,质量为m的小球固定在长为L的细轻杆的一端,绕细杆的另一端O在竖直平面上做圆周运动.球转到最高点A时,线速度的大小为